A ladder 36m long rests against a wall, its foot being at a horizontal distance of 25m from the base of the wall. What angle does the ladder make with the ground?

Question

8973 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-07T11:29:01

The ladder makes #46.02^0# angle with the ground.

In the right triangle formed by the ladder, wall and ground, base is

#b=25# m , hypotenuse is #h=36# m. Let the angle formed by the

ladder with the ground is #theta :. cos theta= b/h=25/36#

#:. theta=cos^-1(25/36) or theta ~~ 46.02^0#

The ladder makes #46.02^0# angle with the ground. [Ans]

Answer 2 · 2018-03-07T11:35:45

#0.803" radians"color(white)("xx")=color(white)("xx")46.0^circ# (approx.)

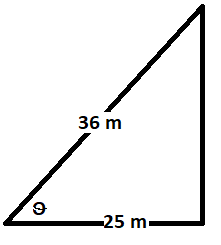
enter image source here

By basic trig definitions (for the above diagram):
#color(white)("XXX")cos(theta)=25/36#
and
#color(white)("XXX")arccos(25/36)=theta#

That is
#color(white)("XXX")theta=arccos(25/36)=arccos(0.69bar4)=0.803" radians"# (using a calculator to 3 decimal places)