Question

A plane is 120 miles north and 85 miles east of an airport. If the pilot wants to fly directly back to the airport, what angle should be taken?

Answer 1

The plane has to turn `125.31°` right to fly directly back towards the airport.

This would be on a bearing of `215°`

Explanation:

We can firstly map out how far north and east the pilot was from the airport, to find the angle to get back to the Airport.

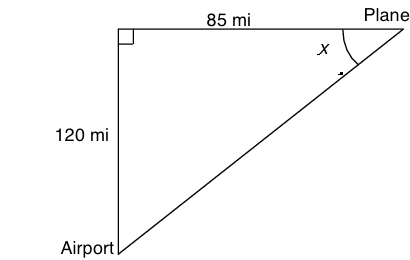
(not to scale)

`x = tan^-1 (120/85)" "`see note below

`x = 54.69º`

Because the plane is flying due east, it has to turn 90º to face south, before it turns the extra `35.31º` to fly towards the airport.

`90° + 35.31° = color(blue)(125.31º)`

It actually turns through the exterior angle of the triangle :
`180-54.69° = 125.31°`

The question would be better if it asked for the bearing.
(Which is what a pilot would use)

Note: `tan^-1` is read as `"arctan:` (to find an angle from the ratio)

and is not the same as `1/tan` which would be `cot`