A triangle has sides A, B, and C. Sides A and B have lengths of 4 and 3, respectively. The angle between A and C is #(11pi)/24# and the angle between B and C is # (3pi)/8#. What is the area of the triangle?
1 Answer
Mar 29, 2018
Explanation:
Using the Law of Cosines we can find the other side, and then the area.
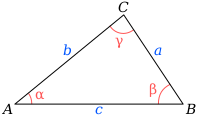
Law of Cosines equation is
From the given angles, the third angle is
We now use Heron's formula for the area:
where
http://mste.illinois.edu/dildine/heron/triarea.html
https://www.mathopenref.com/heronsformula.html

