A triangle has sides A, B, and C. The angle between sides A and B is #pi/12# and the angle between sides B and C is #pi/12#. If side B has a length of 3, what is the area of the triangle?
1 Answer
Dec 23, 2015
Area
Explanation:
(see diagram)
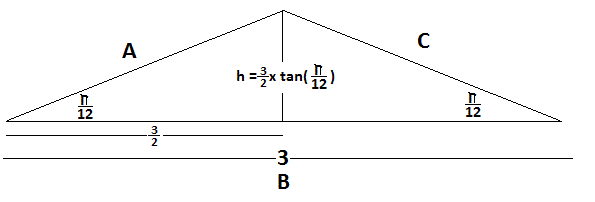
By Half Angle Formula for
using standard values for
The height of the triangle is
and the area is
