A triangle has sides A, B, and C. The angle between sides A and B is #pi/3# and the angle between sides B and C is #pi/12#. If side B has a length of 1, what is the area of the triangle?
1 Answer
Jan 19, 2016
Explanation:
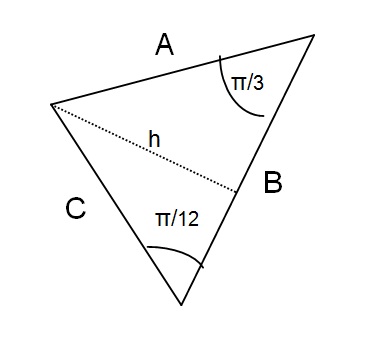
The area of a triangle
In this case the base
If we name the two portions of the base on either side of the perpendicular
We then use the trigonometric relations
We now have three equations and three unknowns so we can solve to find

