A triangle has sides with lengths: 7, 2, and 14. How do you find the area of the triangle using Heron's formula?
2 Answers
Mar 27, 2018
No area
Explanation:
The triangle has no area, and it cannot exist.
The triangle inequality states that,
In words, the sum of a triangle's two sides' lengths is always bigger than the remaining one.
But here, we get:
Mar 27, 2018
Explanation:
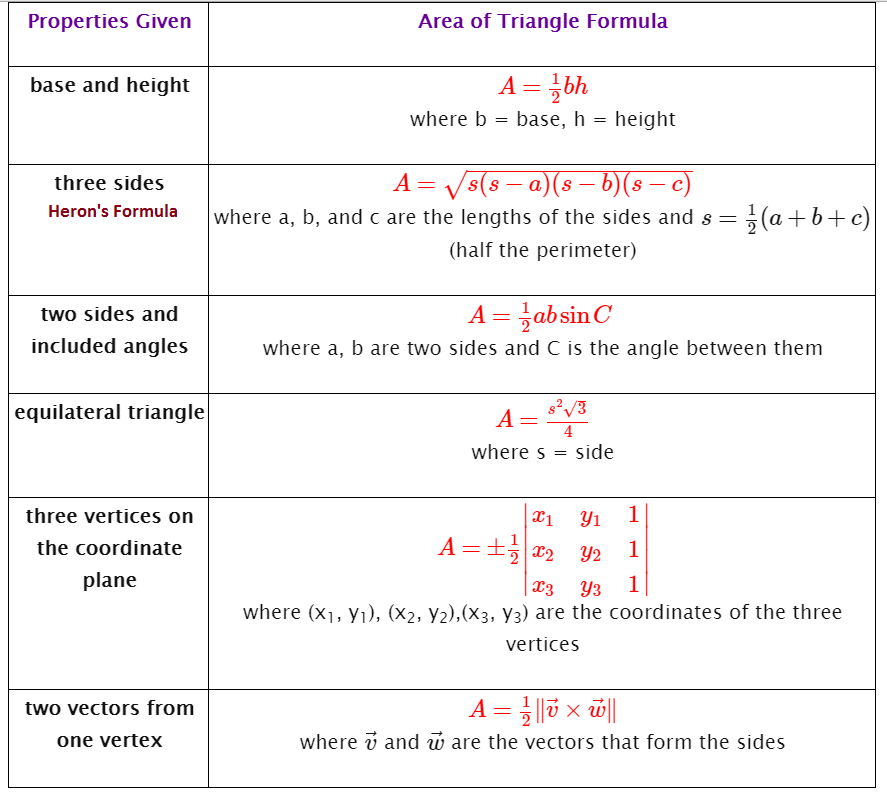
Given :
To find the area of the triangle using Heron's Formula.
Heron's Formula
In this case,

