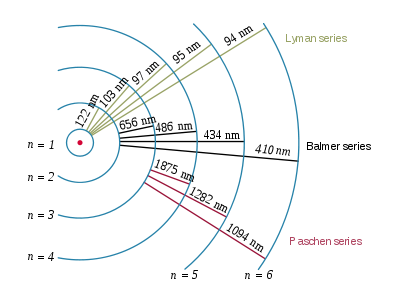
An excited hydrogen atom with an electron in the n = 5 state emits light having a frequency of #6.90 xx 10^14 s^-1#. What is the principal quantum level for the final state in this electronic transition?
1 Answer
Explanation:
The first thing that you need to do here is to use the frequency of the emitted photon to calculate its wavelength.
As you know, frequency and wavelength have an inverse relationship described by the equation
#color(blue)(ul(color(black)(nu * lamda = c)))#
Here
#nu# is the frequency of the photon#c# is the speed of light in a vacuum, usually given as#3 * 10^8# #"m s"^(-1)#
Plug in your value to find
#lamda = (3 * 10^8color(white)(.)"m" color(red)(cancel(color(black)("s"^(-1)))))/(6.90 * 10^(14)color(red)(cancel(color(black)("s"^(-1))))) = 4.348 * 10^(-7)# #"m"#
Now, the relationship between the wavelength of the emitted photon and the principal quantum numbers of the orbitals from which and to which the transition is being made is given by the Rydberg equation
#1/(lamda_"e") = R * (1/n_1^2 - 1/n_2^2)#
Here
#lamda_"e"# is the wavelength of the emitted photon (in a vacuum)#R# is the Rydberg constant, equal to#1.097 * 10^(7)# #"m"^(-1)# #n_1# represents the principal quantum number of the orbital that is lower in energy#n_2# represents the principal quantum number of the orbital that is higher in energy
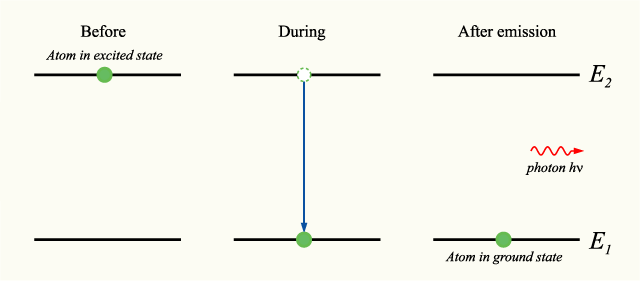
Now, you know that your electron emits an electron, so right from the start, you know that the principal quantum number of the orbital that is higher in energy will be
In other words, the principal quantum number of the final orbital in this transition must be
So, rearrange the Rydberg equation to isolate
#1/(lamda_ "e") = R/n_1^2 - R/n_2^2#
#R/n_1^2 = 1/(lamda_ "e") + R/n_2^2#
#R/n_1^2 = (n_2^2 + lamda_ "e" * R)/(lamda_ "e" * n_2^2) implies n_1 = sqrt((R * lamda_ "e" * n_2^2)/(n_2^2 + lamda_ "e" * R))#
Plug in your values to find
#n_1 = sqrt(( 1.097 * color(blue)(cancel(color(black)(10^7))) color(red)(cancel(color(black)("m"^(-1)))) * 4.348 * color(blue)(cancel(color(black)(10^(-7))))color(red)(cancel(color(black)("m"))) * 5^2)/(5^2 + 4.348 * color(blue)(cancel(color(black)(10^(-7))))color(red)(cancel(color(black)("m"))) * 1.097 * color(blue)(cancel(color(black)(10^7)))color(red)(cancel(color(black)("m"^(-1))))))#
#n_1 = 2.001384 ~~ 2#
Therefore, you can say that your electron is undergoing a