Can 50mm, 13mm and 12mm be a right triangle?
4 Answers
I do not think so.
Explanation:
Try with Pythagora's Theorem:
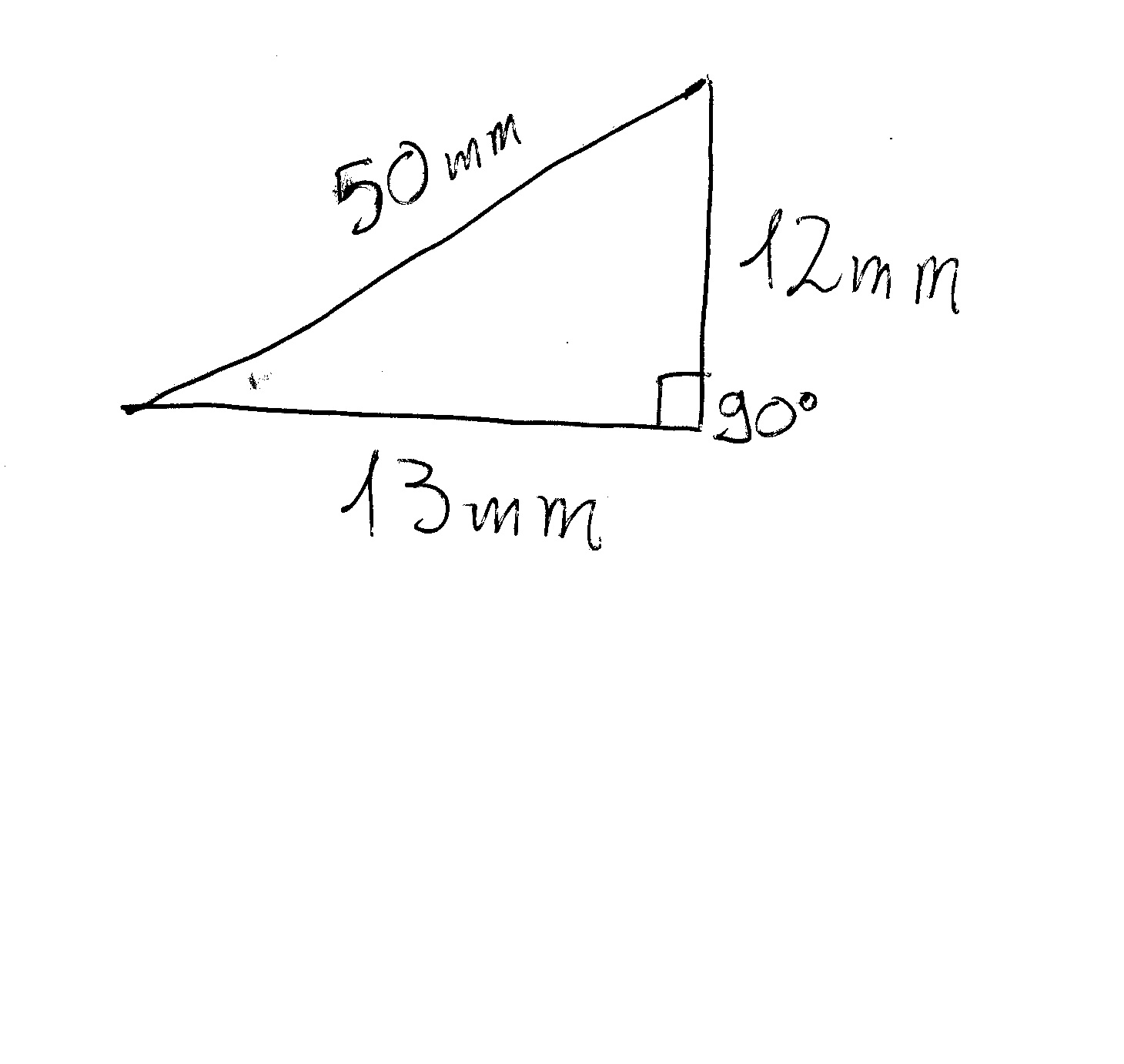
It cannot even be a triangle let alone a right angled one.
Explanation:
If
A triangle with sides 50mm, 13mm, and 12mm can not form a right triangle
Explanation:
By the Pythagorean Theorem, to be a right triangle:
the square of the longest side
must be equal to
the sum of the squares of the other two sides
Also
Note that no triangle can exist with sides 50mm, 13mm, and 12mm.
Explanation 2:
To form a triangle, every side must be less than the sum of the other two sides.
Picture a line segment of length 50mm with a line segment of 13 mm attached to one end and a line segment of 12 mm attached to the other end. The 13mm and 12mm line segments can not reach far enough to touch each other.
No, not according to the Pythagorean theorem.
Explanation:
If you plug in the side lengths into the Pythagorean theorem, assuming that



