From point 135 feet from the base of a tree, the angle from ground level to the top of the tree is 49* (degrees), how do you find the height of the tree?

Question

2952 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-03T02:07:08

The height of the tree is #"155.3 feet"#.

This involves trigonometric ratios. A key concept of remembering how to do this is learning soh-cah-toa. Strange right?

It helps to find sine, cosine, and tangent. For

#"Sin"= "opposite"/"hypotenuse"#

#"Cos" = "adjacent"/"hypotenuse"#

#"Tan" = "opposite"/"adjacent"#

It helps to draw out a picture .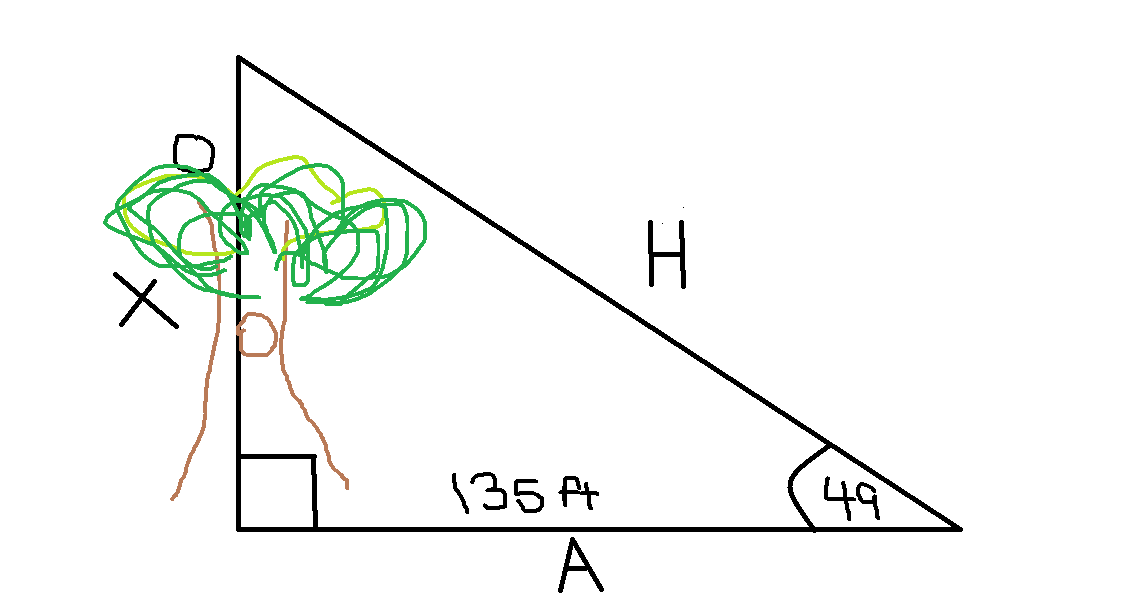 enter image source here Ignore the poor drawing skills. Anyways, you can see it forms a right triangle.

When it labeled, you see we'll be using tangent, which is opposite over adjacent to find #x# (the height of the tree). Set up a proportion.

#Tan(49)/ 1 = x/135#

Cross-mulitiply and you get

#x = 135 times Tan(49)#

Plug that into the calculator and you get #155.299734974836#. Rounded to the nearest tenth, it is #"155.3 feet"#.