How do I use a sign chart to solve #2< -16t^2+6<5#?

Question

3102 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-06-30T21:10:21

#2 < -16t^2+6 < 5# in the intervals (-0.5, -0.25) and (0.25, 0.5).

Here, we have two inequalities that must be satisfied.

(1) #2 < -16t^2+6 # and
(2) #-16t^2+6 < 5#

(1) The first inequality

We write the inequality in standard form by putting all non-zero terms on the left side.

#16t^2-6 +2 < 0#
#16t^2-4 < 0#

We start by finding the critical numbers.

Set #f_1(t) = 16t^2-4 = 0# and solve for #t#.

#4t^2-1 = 0#

#(2t+1)(2t-1) = 0#

#2t+1 = 0# or #2t-1 = 0#

#t=-0.5# or #t=+0.5#

The critical numbers are #-0.5# and #+0.5#.

We have three intervals to consider: (-∞, -0.5), (-0.5, 0.5), and (0.5, ∞).

We pick a test number and evaluate the function and its sign at that number.

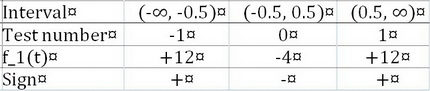
enter image source here

(2) The second inequality

The inequality in standard form is

#-16t^2+6 -5 < 0#
#-16t^2+1 < 0# or #1-16t^2 <0#

Set #f_2(t) = 1-16t^2 = 0# and solve for #t#.

#(1+4t)(1-4t) = 0#

#1+4t = 0# or #1-4t = 0#

#t=-0.25# or #t=+0.25#

The critical numbers are #-0.25# and #+0.25#.

The three intervals to consider are: (-∞, -0.25), (-0.25, 0.25), and (0.25, ∞).

enter image source here

Now we create a sign chart for the two functions.

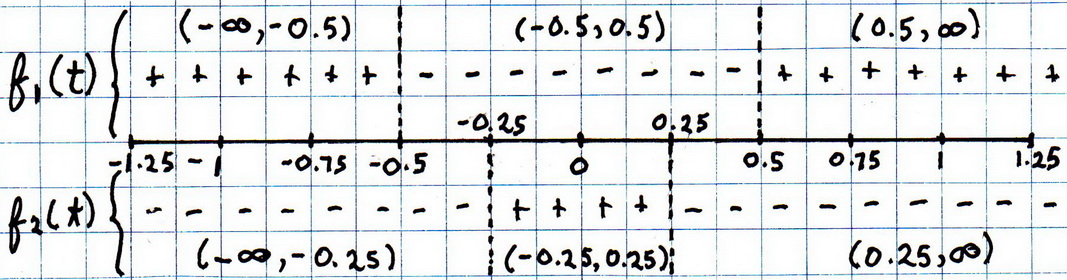
enter image source here

The only intervals for which the two signs are both negative are (-0.5, -0.25) and (0.25, 0.5).