How do I use a sign chart to solve #x^2<4#?
1 Answer
Jun 30, 2015
Explanation:
Let's modify the inequality by subtracting
We start by finding the critical numbers.
Set
The critical numbers are
Now we check for positive and negative regions.
We have three regions to consider: (a)
Case (a): Let
Then
Case (b): Let
Then
Case (c): Let
Then
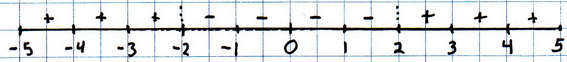
If

