How do we find the apothem of a regular polygon?
1 Answer
Apothem of a regular polygon with
Explanation:
Apothem is the line joining the center of a regular polygon to the middle point any of its side. It is also the radius of incircle of the regular polygon.
Assume there are
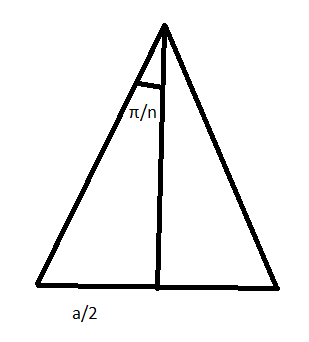
and if apothem is
and hence apothem is
Hence, apothem of a regular polygon with
