In order to convert between cartesian and polar coordinates, we have to use Pythagoras' theorem.
Consider the point #(5, -2)#, which is the point you're trying to convert from cartesian to polar form. The Polar form gives direction and distance to any point on a graph, so that's what we'll do for 5-2#i#. Let's use this graph to explain how to do that: 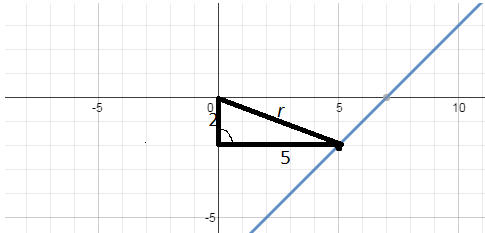
In order to convert #5 - 2i# to polar form, you'll have to work out the value of #r#, the distance, and the size of the angle #theta#, the direction. Using Pythagoras' theorem, we can work that #r^2 = 5^2+ 2^2 = 29#, so #r=sqrt(29) = 5.4#
Now, to work out #theta#, we have to work out the radial angle from the positive #x#-axis to #r#. (There's a mistake in the picture; apologies about that.) Let's look at this picture now:
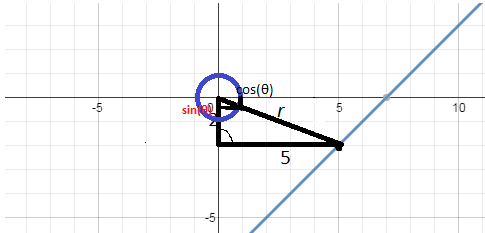
Using a unit circle, we can easily figure out the radial coordinates of where #r# touches the unit circle. But this isn't what we're interested in; we want the coordinates of #5-2"i"#.
To obtain this, though, is very simple. If where #r# touches the unit circle has #x#-coordinate #cos(theta)# and #y# coordinate #sin(theta#), then #5-2i# has #x# coordinate #rcos(theta)# and #y# coordinate #rsin(theta)#. (We can equate these to their cartesian coordinates, too.)
Now, to evaluate these two, we need to put them into a trigonometric function. In this case, we will use #tantheta# #=# #sintheta/costheta#. Using our #r# values, we get the equation: tan#theta# #=# #r##sintheta/costheta# = #-2/5#. Therefore, #theta# #= tan^-1##(-2/5) # #= -21.8#



