How do you convert # sqrt(3)+i# to polar form?
2 Answers
Jun 23, 2016
I found:
Explanation:
Have a look:
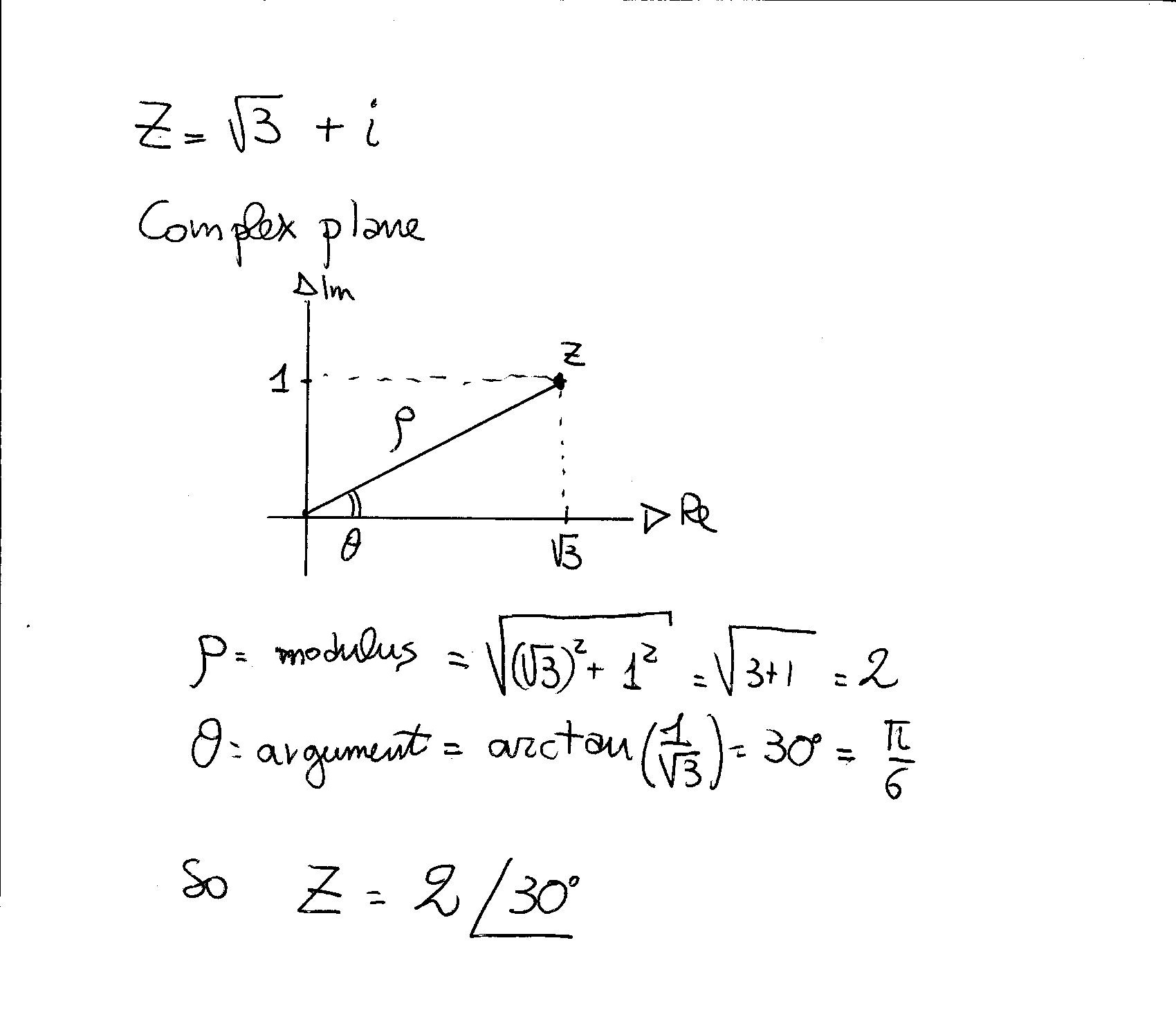
Jun 23, 2016
Explanation:
To convert cartesian coordinates (x ,y) to Polar coordinates
#(r,theta)#
Use the formulae which link them.
#•r=sqrt(x^2+y^2)# and since
#sqrt3+i=(sqrt3,1)# is in the 1st quadrant , then.
#•theta=tan^-1(y/x)# here x =
#sqrt3" and "y=1#
#rArrr=sqrt((sqrt3)^2+1^2)=sqrt4=2# and
#theta=tan^-1(1/sqrt3)=pi/6" or "30^@#
#rArr(sqrt3,1)to(2,pi/6)#

