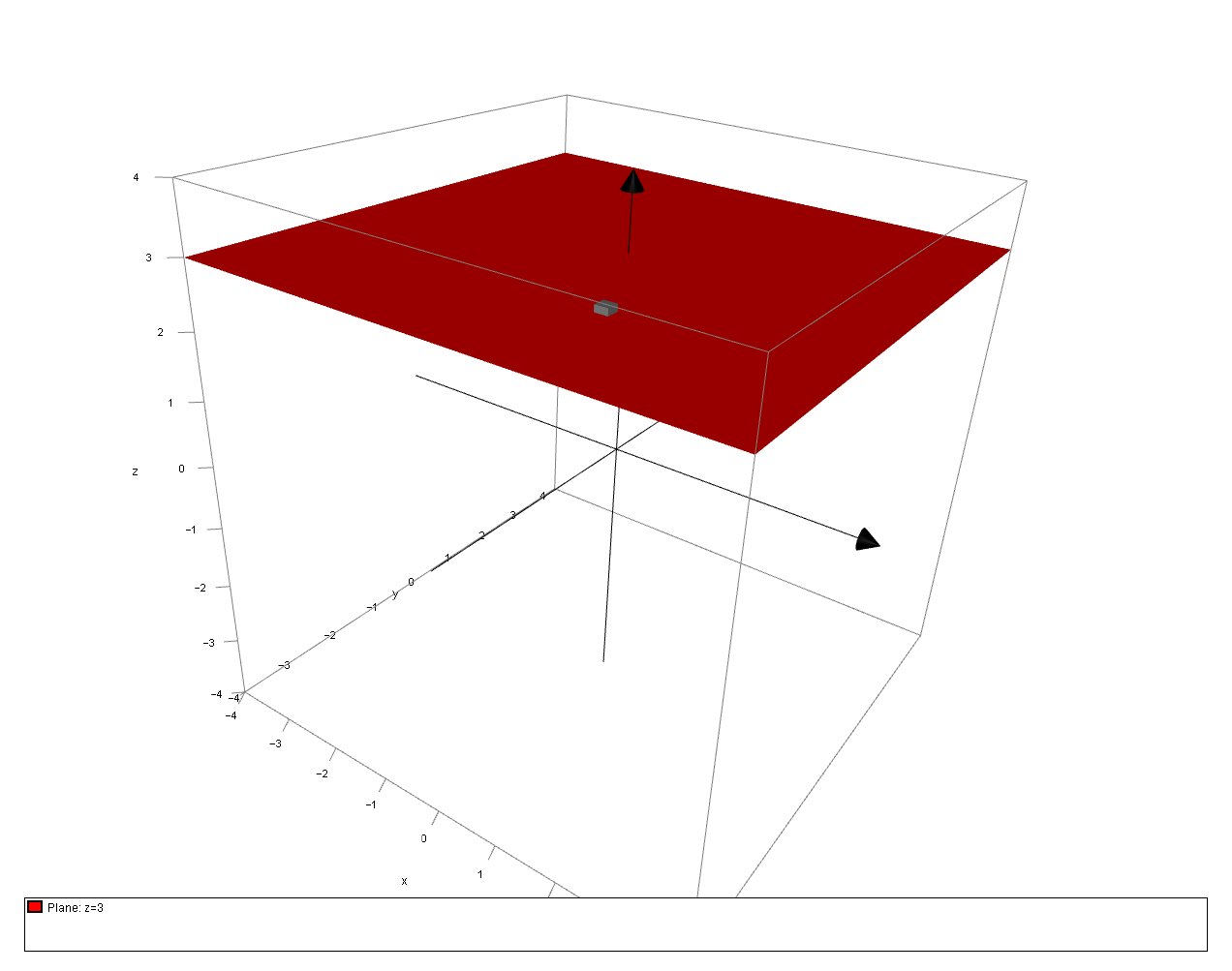
How do you determine the vector and parametric equations for the plane through point (1, -2,3) and parallel to the xy-plane?

Question

5002 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-03-31T00:38:47

# z=3# and # vecr * ( (0), (0), (1) ) = 3 #

Any plane that is parallel to the #xy#-plane is perpendicular the the #z#-axis. ie it has a normal vector given by:

# vec n = ( (0), (0), (1) ) #

Hence the plane has an equation of the form:

# 0x+0y+1z = k => z=k #

we want the plane to pass through #(1,-2,3)# and so
#k=3#

Hence the required plane equation is

# z=3#

For the vector equation we use the form:

# (vecr-vecr_0) * vecn = 0 => vecr * vecn = vecr_0 * vecn #

which gives us:

# vecr * ( (0), (0), (1) ) = ( (1), (-2), (3) ) * ( (0), (0), (1) ) #

# :. vecr * ( (0), (0), (1) ) = 3 #

We can show this on a 3D plot:
enter image source here