How do you evaluate #arctan((1/sqrt3)#?
1 Answer
Jul 22, 2015
Explanation:
This ratio is one of the standard trigonometric triangles:
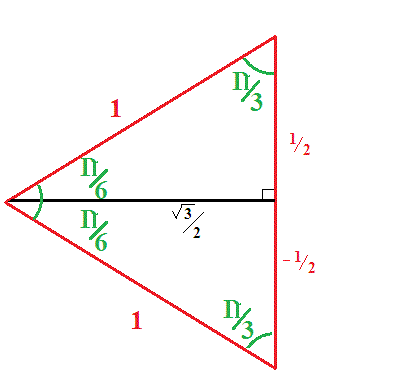
The ratio
This ratio is one of the standard trigonometric triangles:

The ratio