How do you evaluate #sin(cos^-1(1/2))# without a calculator?
2 Answers
Mar 5, 2018
Explanation:
Let
Now,
Mar 5, 2018
Explanation:
To find value of
Let theta = cos^-1 (1/2)#
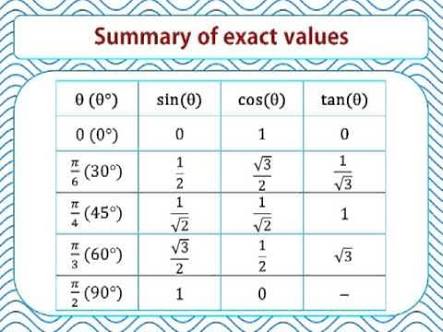
We know, from the above table,
Hence theta = 60^@#
Replacing
The sum becomes,

