How do you expand #(1+x^3)^4# using Pascal’s Triangle?
1 Answer
Since there are (4 + 1) = 5 terms in this expansion, we must find the numbers located in the
Explanation:
Draw a diagram to represent Pascal's Triangle. Each row is the sum of the numbers above it, with 1 at the first row, (1 and 1) at the second row, (1, 2 and 1) in the third row. The following diagram is of Pascal's Triangle:
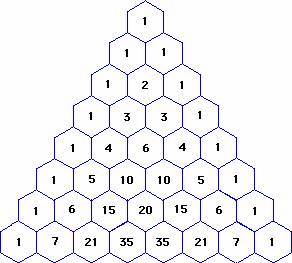
Counting up from the row with a single 1, we find that row 5 contains the numbers 1, 4, 6, 4 and 1.
To expand, the exponents on the 1 will start at 4 and will decrease until 0. The exponents on the
Simplifying by using exponent laws:
When fully expanded,
Practice Exercises:
-
Expand
#(2x - 3y)^5# using Pascal's Triangle. -
Find the 3rd term in
#(x + 3)^7# . Hint: Think of finding the appropriate number in the Pascal's Triangle and plugging it in for nCr in#t_(r + 1) = nCr(a)^(n - r) xx b^r# .
Good luck!

