Question

How do you factor #y=x^3+8x^2+17x+10 #?

Answer 1

To get started, you will have to find a factor. This can be long. Use the remainder theorem to test possible factors. The possible factors are given by the rational root theorem. See below for more details.

Explanation:

The rational root theorem states that in a polynomial `ƒ(x) = qx^n + mx^(n - 1) + ... + px^0`, the possible roots will be at `p/q`.

Therefore, we can state that the possible roots are at (factors of 10)/(factors of 1). Listing these, we get:

`(+- 1, +-2, +-5, +-10)/(+-1)`

Simplifying further:

`+-1, +-2, +-5, +-10`

Here comes the part that can be long. The remainder theorem states that for any polynomial function `p(x)` being divided by `x - a)`, the remainder is given by evaluating `p(a)`. A factor, when evaluated, will give a final result, or a remainder, of 0, since by definition a factor is a number that evenly divides another.

When I do this, I tend to go from positive to negative, from smallest to largest. From experience, it is relatively rare for you not to find a factor by `(x + 2)`. Following my technique, we will start with `(x - 1)` and then proceed with `(x + 1)`. Inspect the following proofs:

`y = (1)^3 + 8(1)^2 + 17(1) + 10`

`y = 1 + 8 + 17 + 10`

`y = 36`, therefore, `(x - 1)` is not a factor of this polynomial.

`y = (-1)^3 + 8(-1)^2 + 17(-1) + 10`

`y = -1 + 8 - 17 + 10`

`y = 0`

Therefore, `(x + 1)` is a factor of this polynomial.

We must now divide `(x^2 + 8x^2 + 17x + 10)` by `(x + 1)` to see what is left over.

The following image shows the long division (you could have also used synthetic division).

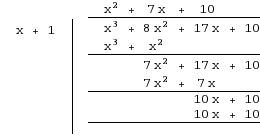
As you can see, the quotient is `x^2 + 7x + 10`

This can easily be factored by finding two numbers in `y = ax^2 + bx + c, a = 1` that multiply to c and that add to b. Two numbers that do this are `5 and 2`

Therefore,

`y = x^3 + 8x^2 + 17x + 10 = (x + 1)(x + 5)(x + 2)`

or

`y = (x + 1)(x + 5)(x + 2)`

Hopefully this helps!