Monomial Factors of Polynomials
Key Questions
-
Answer:
As elaborated.
Explanation:
A polynomial is factored completely when it is expressed as a product of one or more polynomials that cannot be factored further.
Not all polynomials can be factored. To factor a polynomial completely: Identify and factor out the greatest common monomial factor
-
Break down every term into prime factors.
-
Look for factors that appear in every single term to determine the GCF.
-
Factor the GCF out from every term in front of parentheses and group the remnants inside the parentheses.
-
Multiply each term to simplify.
Few examples are given below to find the GCF.
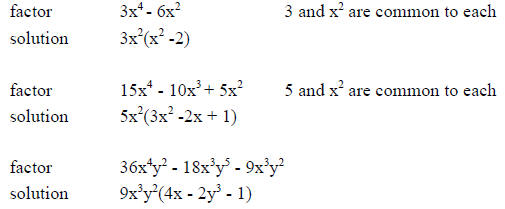
-
-
You can check your factoring by multiplying them all out to see if you get the original expression. If you do, your factoring is correct; otherwise, you might want to try again.
I hope that this was helpful.
-
Answer:
As described in the image enclosed
Explanation:
Step by step method to find the greatest common factor :
-
Look at the coefficients
-
look at the variables.
-
Identify the GCF

-
-
Answer:
The 'normal' way of finding the GCF of two polynomials is to factor both of them completely, then pick out the common factors and multiply them together.
Alternatively you can use division.
Explanation:
Normal Method - Factor both polynomials first
For example:
Given
f(x) = x^2+6x+9 andg(x) = x^2+x-6 ,you can factor
f(x) = (x+3)^2 andg(x) = (x+3)(x-2) hence the GCF is
(x+3) Backup Method - Using division of polynomials
Given:
f(x) = x^4+2x^3+4x^2+3x+2
and:g(x) = x^4+3x^3+6x^2+5x+3 If
f(x) andg(x) have a common polynomial factorp(x) then if we dividef(x) byg(x) (or vice versa), the remainder must be a multiple ofp(x) .For example,
g(x) = f(x) + (x^3+2x^2+2x+1) Let
h(x) = x^3+2x^2+2x+1 If we now divide
f(x) byh(x) then any remainder will also be divisible byp(x) :x^4+2x^3+4x^2+3x+2 = (x^3+2x^2+2x+1)x+2x^2+2x+2 =h(x)*x + 2(x^2+x+1) Next try dividing
f(x) byx^2+x+1 ...x^4+2x^3+4x^2+3x+2 = (x^2+x+2)(x^2+x+1) This time there is no remainder, so
p(x) = x^2+x+1 is our GCFFor a more complex example, see http://socratic.org/questions/if-you-are-told-that-x-7-3x-5-x-4-4x-2-4x-4-0-has-at-least-one-repeated-root-how
Questions
Polynomials and Factoring
-
Polynomials in Standard Form
-
Addition and Subtraction of Polynomials
-
Multiplication of Monomials by Polynomials
-
Multiplication of Polynomials by Binomials
-
Special Products of Polynomials
-
Monomial Factors of Polynomials
-
Zero Product Principle
-
Factorization of Quadratic Expressions
-
Factor Polynomials Using Special Products
-
Factoring by Grouping
-
Factoring Completely
-
Probability of Compound Events