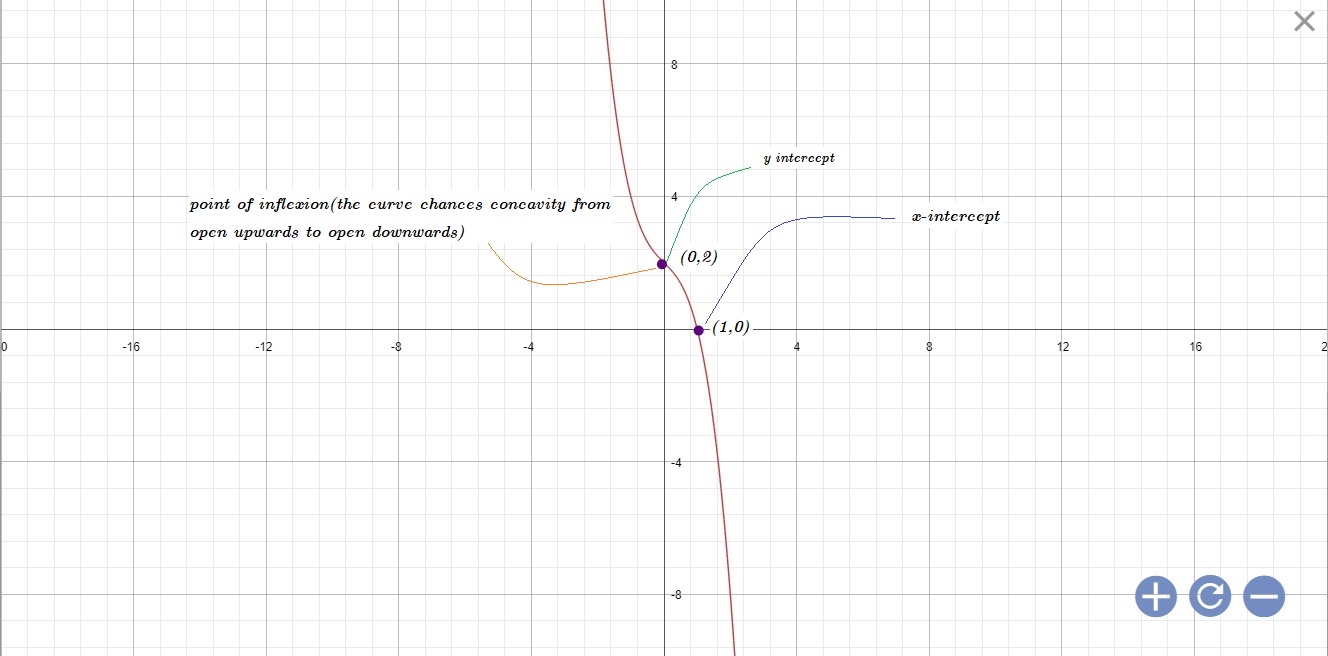
How do you find intercepts, extrema, points of inflections, asymptotes and graph #y=2-x-x^3#?
1 Answer
read the explanation
Explanation:
To find intercepts:
x intercept means "the point where the graph cuts x-axis".At this point the y co-ordinate will be 0(the point will have form
similarly, at y intercept x=0;
now put x=0 in equation to find y intercept
and put y=0 in equation to find x intercept
from the question,
thus y intercept is at point
similarly putting y=0 we'll get x intercept(s)
for extrema and points of inflexion use derivative method
the point(s) where the first derivative of the equation is 0(or the points where the slope of curve is 0) are called critical point(s)
on differentiating
hence the curve will have no critical point
also as
the function
for points of inflexion (the point where curve changes concavity or shape) the second derivative must be 0
we have second derivative as
since,
it has no asymptotes
it will be more clear from the graph