Question

How do you find intercepts, extrema, points of inflections, asymptotes and graph `y=(20x)/(x^2+1)-1/x`?

Answer 1

There is a vertical asymptote at `x=0`
There is a horizontal asymptote as `x rarr +- oo` along the `x`-axis
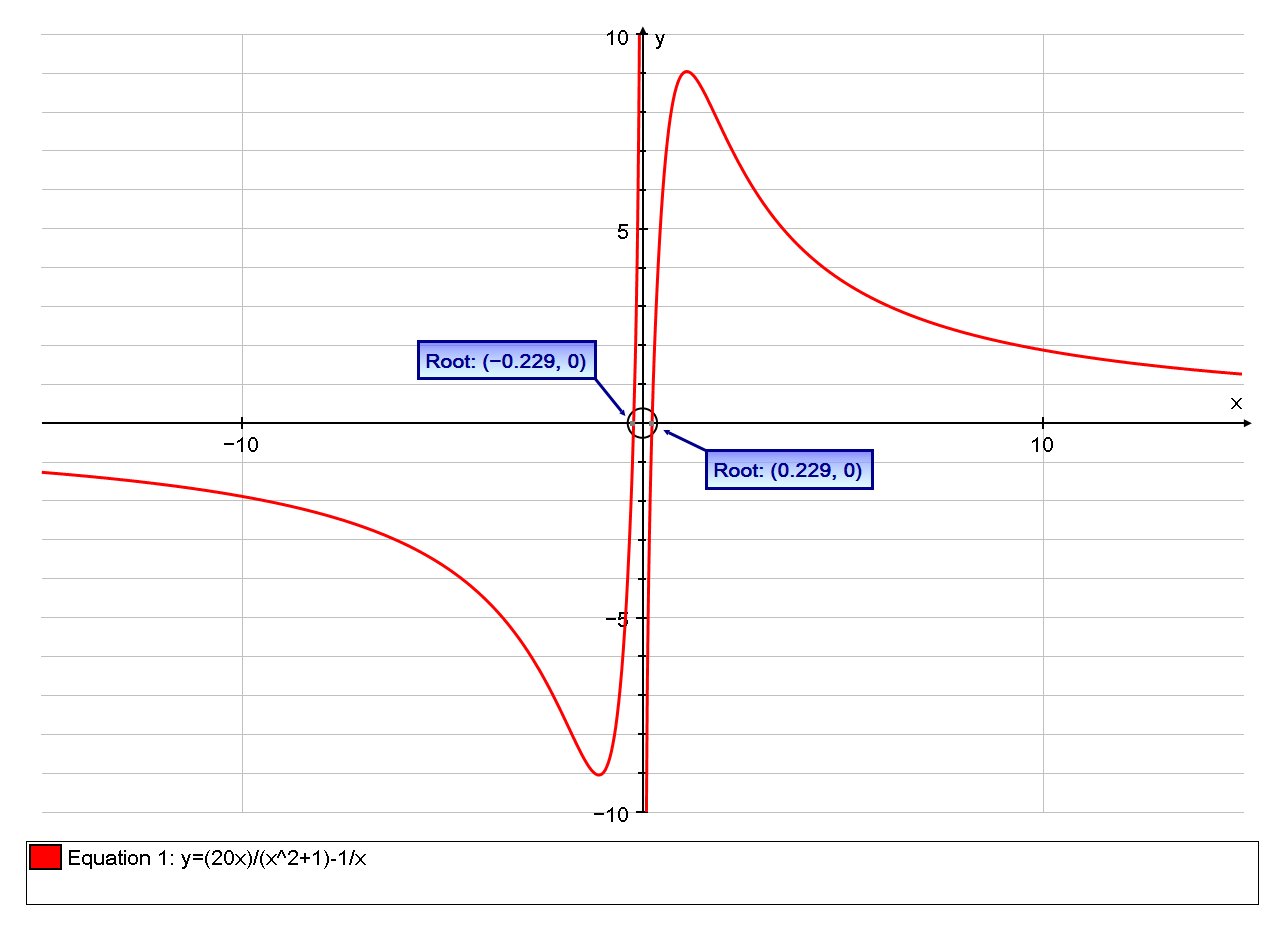
x-intercepts when `x=+-1/sqrt19`
y(x) is an odd function, and it is symmetric about the origin O

Critical points are:
Maximum at `(1.096, 9.046)`
Minimum at `(-1.096, -9.046)`

Explanation:

`y=(20x)/(x^2+1)-1/x`
`:. y=((20x^2)-(x^2+1))/(x(x^2+1))`
`:. y=(19x^2-1)/(x(x^2+1))`

Vertical Asymptotes
These will occur when the denominator is zero

`:. x(x^2+1)) =0 => x=0`

So There is a vertical asymptote at `x=0`

Horizontal Asymptotes
We need to examine the behaviour as `x rarr +- oo`.
For large `x`,
`19x^2-1 ~ x^2`
`x^2+1 ~ x^2`
So, `(19x^2-1)/(x(x^2+1)) ~ 19x^2/x^3 ~ 1/x ->0` as `x rarr +- oo`
So There is a horizontal asymptote as `x rarr +- oo` along the `x`-axis

Odd/Even Function
Find y(-x);

`y(-x)=(19(-x)^2-1)/(-x((-x)^2+1))`
`y(-x)=(19x^2-1)/(-x(x^2+1))`
`y(-x)=-(19x^2-1)/(x(x^2+1))`
`y(-x)=-y(x)`

Hence y(x) is an odd function, and it is symmetric about the origin O

Intercepts

`y=(19x^2-1)/(x(x^2+1)) => 19x^2-1 = 0`
`:. x^2=1/19`
`:. x^2=+-1/sqrt19 ~~~ +- 0.229`

We have already established that x=0 is a vertical asymptotes so there are not y-axis intercepts.
Hence x-intercepts when `x=+-1/sqrt19`

Summary
There is a vertical asymptote at `x=0`
There is a horizontal asymptote as `x rarr +- oo`
y(x) is an odd function, and it is symmetric about the origin O

Extrema
Because of symmetry we only need to identify extra for `x>=0`
We can write;

`y=(19x^2-1)/(x^3+x)`

Using the quotient rule

`y=(19x^2-1)/(x^3+x)`
`dy/dx=((x^3+x)(d/dx(19x^2-1)) - (19x^2-1)(d/dx(x^3+x)) )/(x^3+x)^2`
`:. dy/dx=((x^3+x)(38x) - (19x^2-1)(3x^2+1) )/(x^3+x)^2`
`:. dy/dx=(38x^4+38x^2 - (57x^4+16x^2-1) )/(x^3+x)^2`
`:. dy/dx=(38x^4+38x^2 - 57x^4-16x^2+1 )/(x^3+x)^2`
`:. dy/dx=(-19x^4+22x^2 +1 )/(x^3+x)^2`
`:. dy/dx=-((19x^4-22x^2 -1 ))/(x^3+x)^2`

At extrema, `dy/dx=0 => 19x^4-22x^2 -1 =0`
This is quadratic in `x^2` and can be solved, which I will return to!
To solve this we use the quadratic formula

`x=(-b+-sqrt(b^2-4ac))/(2a)`

to find two solutions for `x^2`, and then take their square roots, which yields two real solutions;

`x=+-1.096` (3dp)

Due to the symmetry about O, we only need to examine one of these critical points as the other will be the opposite. Let's look at `x=1.096`

By inspection (using a calculator with `x=1.096+-epsilon`, where `epsilon` is small we can see this point corresponds to a maximum, and so `x=-1.096` is a minimum. We could also investigate using the second derivative test, but due to the complexity a simple computed test is easier.

When `x=1.096 => y=9.046` (3dp)

Hence, Critical points are:
Maximum at `(1.096, 9.046)`
Minimum at `(-1.096, -9.046)`