How do you find limits on a graphing calculator?
1 Answer
I am not sure if there is a TI-84 Plus function that directly finds the value of a limit; however, there is a way to approximate it by using a table. Let us approximate the value of the limit
Step 1: Go to "Y=", then type in the function.
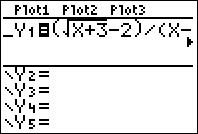
Step 2: Go to "TBL SET" (2nd+WINDOW), then set TblStart=.97 and
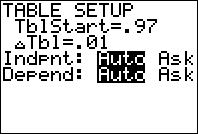
(Note: TblStart is the starting x-value in the table, so put a number slightly smaller that the number x approaches.
Step 3: Go to "" TABLE (2nd+GRAPH).
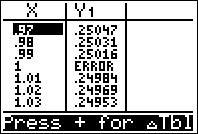
As you can see in the table above, the function value (

