Question

What is the limit as x approaches 0 of `cotx/lnx`?

Answer 1

Since `ln x` is only defined when `x>0`, we can only talk about the right-hand limit:

`lim_{x to 0^+}{cot x}/{ln x}`

Since

`{(lim_{x to 0^+}cot x=lim_{x to 0^+}{cos x}/{sin x}={1}/{0^+}=+infty),(lim_{x to 0^+}ln x=-\infty):}`,

by applying l'H`hat{"o"}`pital's Rule (`infty`/`infty`),

`=lim_{x to 0^+}{-csc^2x}/{1/x}`

by `csc x=1/{sin x}`,

`=-lim_{x to 0^+}x/{sin^2x}`

by l'H`hat{"o"}`pital's Rule (`0"/"0`),

`=-lim_{x to 0^+}1/{2sinx cosx}=-1/0^+=-infty`

The graph of `y={cot x}/{ln x}` looks like:

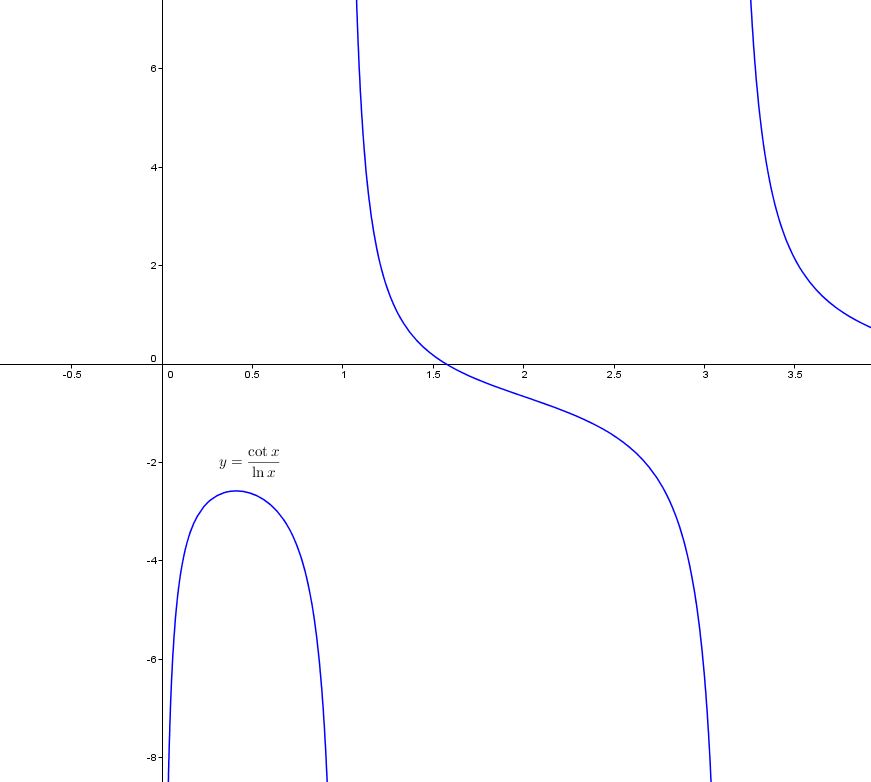
As shown above, as `x` approaches 0 from the right, the graph is shooting down toward `-infty`.