Determining Limits Graphically

Key Questions

  • How do you find limits on a graphing calculator?

    I am not sure if there is a TI-84 Plus function that directly finds the value of a limit; however, there is a way to approximate it by using a table. Let us approximate the value of the limit

    #lim_{x to 1}{sqrt{x+3}-2}/{x-1}#

    Step 1: Go to "Y=", then type in the function.

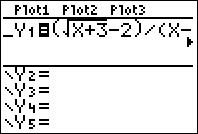
    enter image source here

    Step 2: Go to "TBL SET" (2nd+WINDOW), then set TblStart=.97 and #Delta#Tbl=.01.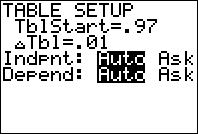

    enter image source here

    (Note: TblStart is the starting x-value in the table, so put a number slightly smaller that the number x approaches. #Delta#Tbl is the increment value in the x-column, so make it sufficiently small for the precision you need.)

    Step 3: Go to "" TABLE (2nd+GRAPH).

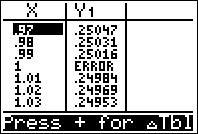
    enter image source here

    As you can see in the table above, the function value (#Y_1#) approaches 0.25 (or 1/4) as x approaches 1; therefore, we conclude that

    #lim_{x to 1}{sqrt{x+3}-2}/{x-1}=1/4#

    Wataru · 4 · Sep 24 2014
  • How do you find #lim_(x->5)(x^2+2)# using a graph?

    If you're using a graph to find this limit, the first thing you'll want to do is graph the function.

    #f(x)=x^2+2# is a parabola that looks like this: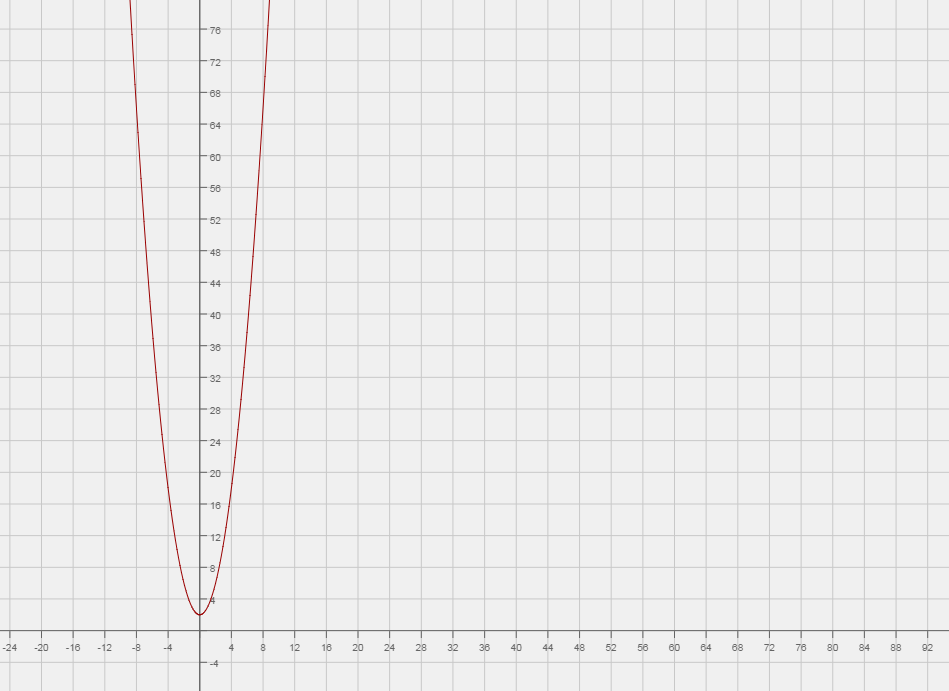

    meta calculator:

    If you want to find out how to graph this, you can either draw the graph of a normal parabola and translate it vertically by two units upwards (2 is being added to the #x^2#, which is why it goes up), or you can create a table of values and plug in input #x# values to get output #y# and you'll get an idea of the shape of the graph.

    Now we're interested in knowing what is happening at #x#=5. Luckily, the function is defined there. If we look at the graph, at #x#=5, y=27. It's a little bit hard to tell on the graph because of the exponentially increasing y-values, but we know that #y#=27 because #y=(5^2+2)=27#. We can plug in #x# directly to find the limit because the function is defined and continuous there.

    To get an idea of an it intuitively means to find a limit on a graph though, you can look at the graph and decide what is happening at #x#=5. When you move to #x#=5 from the right, what is #y# tending to? Well, to 27. Also, when you move to #x#=5 from the left, what is #y# tending it? 27 again. You can think of limits from the right and left as arrows pointing right and left respectively to the #x# value you're looking for. You're kind of trying to "pin point" what is exactly is happening at your graph at that given #x# point. In this case it's quite simply reading the #y# value off the graph, since the left and right limits tend to the same point and therefore are equal.

    So,

    #lim_(x->5) (x^2+2)=27#

    Sally · · Sep 27 2014

Questions

Limits