Question

How do you find parametric equations for the line of intersection of two planes 2x - 2y + z = 1, and 2x + y - 3z = 3?

Answer 1

`vec r = ((7/6), (2/3), (0)) + lambda ((5), (8), (6))`

Explanation:

for the line, we will need

A) a point that it actually passes through, say `vec a`, AND

B) a vector describing the direction in which it travels, say `vec b`

....such that the line itself is

`vec r = vec a + lambda vec b qquad square`

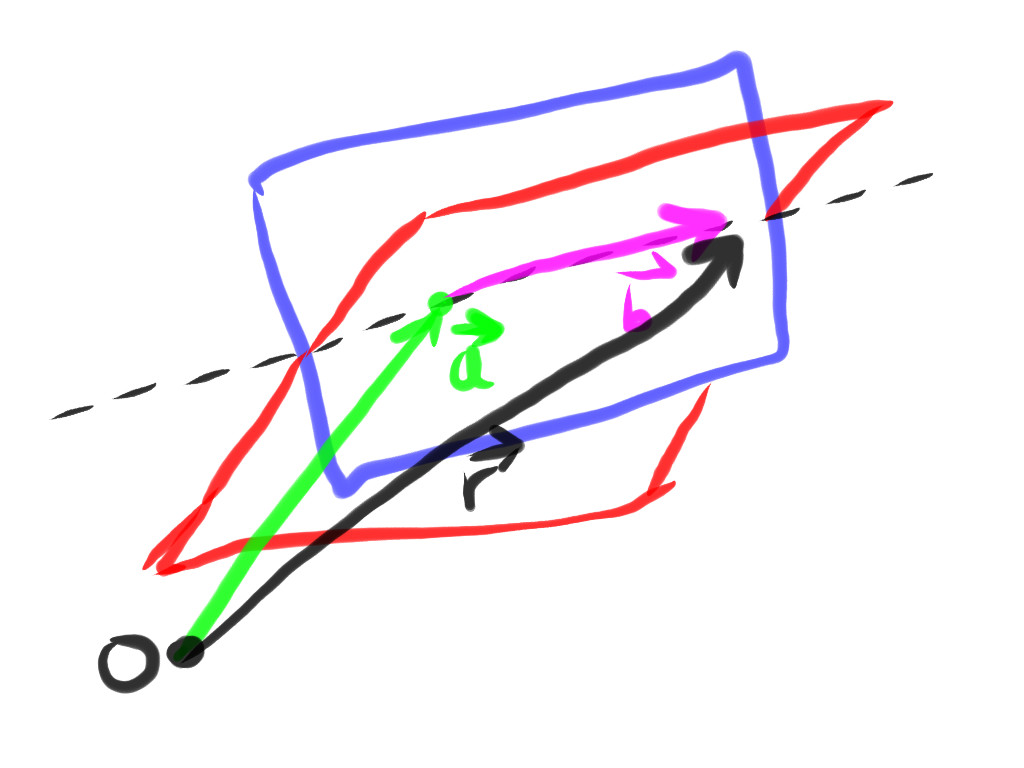
For `vec a`, we can simply choose the completely arbitrary point, so here we choose the point at which z = 0

This means that the plane equations, namely

`pi_1: 2x - 2y + z = 1`

`pi_2: 2x + y - 3z = 3`

become
`2x - 2y = 1`
`2x + y = 3`

and these we solve as simultaneous equations to get

`x = 7/6, y = 2/3` and of course `z = 0`

so `vec a = ((7/6), (2/3), (0))`

for `vec b` we need to calculate the vector cross product of the normal vectors for `pi_1` and `pi_2`.

In the drawing below, we are looking right down the line of intersection, and we get an idea as to why the cross product of the normals of the red and blue planes generates a third vector, perpendicular to the normal vectors, that defines the direction of the line of intersection.

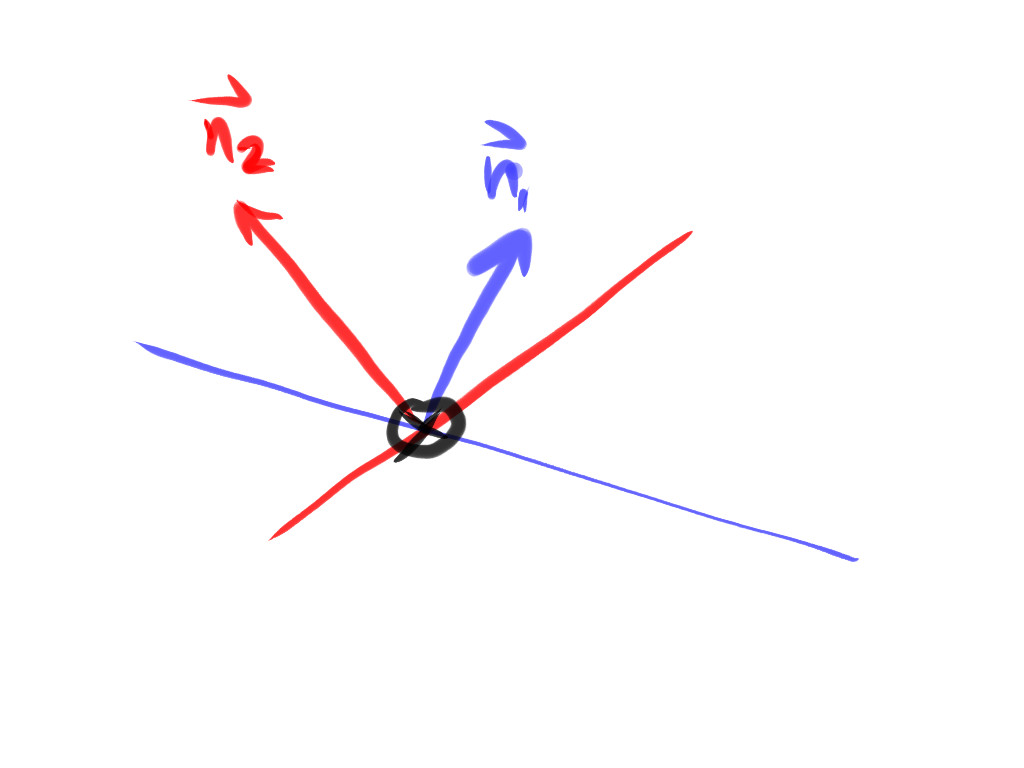
for a generalised plane `pi: ax + by + cz = d`, the normal vector is: `vec n = ((a), (b), (c))`

so for `pi_1: 2x - 2y + z = 1`, the normal vector is `vec n_1 =((2), (-2), (1))`

and for `pi_2: 2x + y - 3z = 3`, the normal vector is `vec n_2 = ((2), (1), (-3))`

the cross product `vec b = vec n_1 times vec n_2` is the following determinant:

`vec b = det [(hat i, hat j, hat k),(2, -2, 1), (2, 1, -3) ]`

`= ((5), (8), (6))`

so we combine this all as indicated in `square` as follows

`vec r = ((7/6), (2/3), (0)) + lambda ((5), (8), (6))`

There are an infinite number of ways of expressing this line. `vec a` can be any point on the line. And the direction vector `vec b` can be any multiple of the one given herein.

The important bit, I guess is the method.