Question

How do you find the area between `f(x)=x+1` and `g(x)=(x-1)^2`?

Answer 1

The area is `9/2` square units.

Explanation:

Start by finding the intersection points of the curves.

`{(y = x+ 1), (y = (x - 1)^2):}`

Solve by substitution.

`x + 1= (x- 1)^2`

`x+ 1 = x^2 - 2x + 1`

`0 = x^2 - 3x`

`0 = x(x - 3)`

`x= 0 and 3`

`0` and `3` are going to be the values of a and b, respectively, in `int_a^b`.

We now draw the two curves to see which one is above and which one is below. This is important, as we will then find the area under the higher curve and subtract the area of the lower curve.

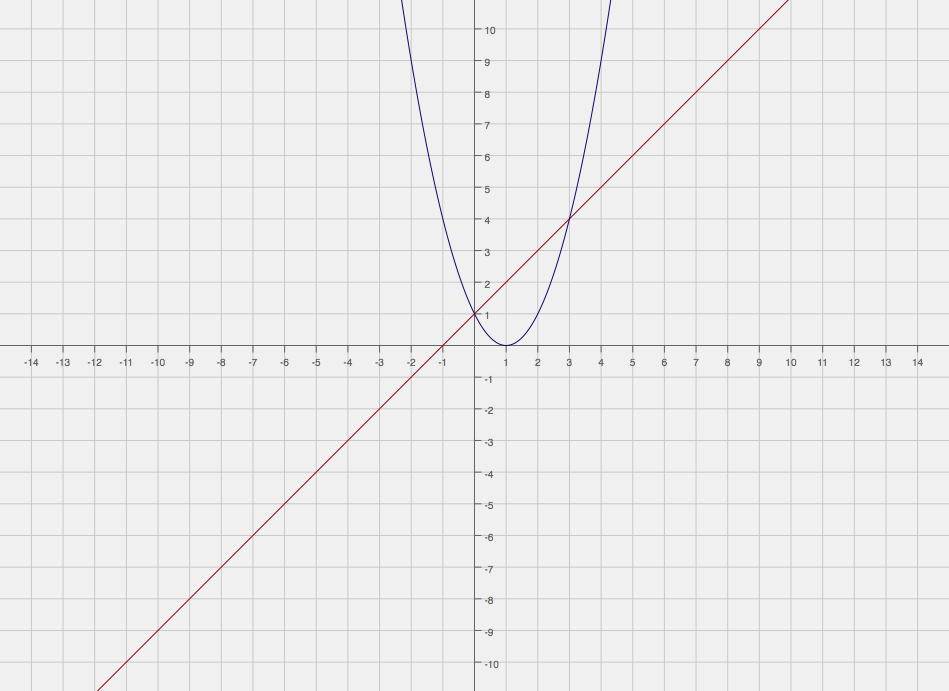
So, we find the area of the linear function (`f(x)`) and then subtract the area of the quadratic (`g(x)`).

`A = int_0^3(x + 1 - (x - 1)^2)dx`

`A = int_0^3(x + 1 - x^2 + 2x - 1)dx`

`A = int_0^3(-x^2 + 3x)dx`

`A = -1/3x^3 + 3/2x^2|_0^3`

`A = -1/3(3)^3 + 3/2(3)^2`

`A = -9 + 27/2`

`A = 9/2`

Hopefully this helps!