How do you find the area bounded by #y=x^2+2x-4# and #y=-2x^2+4x-3#?
2 Answers
Explanation:
Consider the function:
The values of
Note now that as
The area bounded by the curves is then:
Use the integral of the difference between the two functions:
Explanation:
Here is a graph of
and
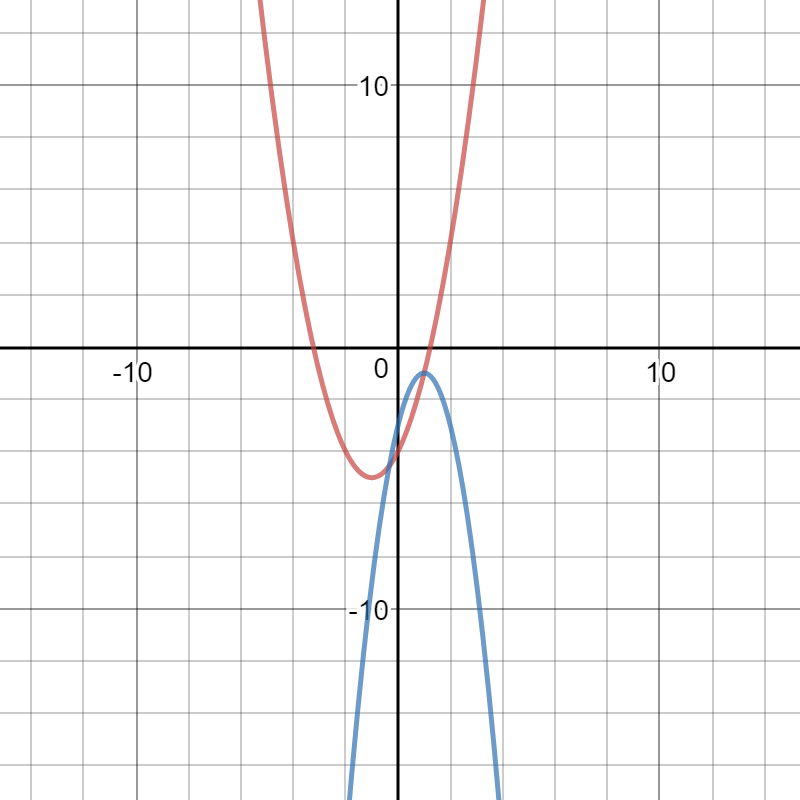
Pleases observe that equation [2] is greater than equation [1] in the enclosed region; this means that the integral is of the form:
Simplify the integrand:
We need to find the values of "a" and "b" by finding the two x coordinates where the two parabolas intersect. We can do this by setting the integrand equal to 0 and then solving for the two values of x:
Multiply by -1:
This factors into:
The above are the values of "a" and "b":

