How do you find the length of the missing side of a right triangle if the hypotenuse is 4sqrt3 and the short side is 2?

Question

2824 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-06-11T00:29:45

I found the length as #6.6#

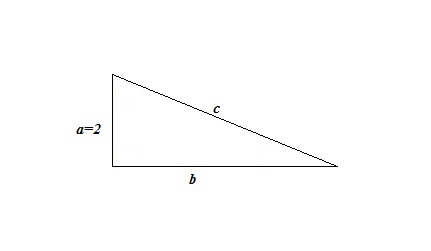
I would use Pythagora's Theorem as:
#c^2=a^2+b^2#
where #c=4sqrt(3)# is the hipotenuse.
So:
#16*3=4+b^2#
#b=sqrt(48-4)=6.6#
enter image source here

Answer 2 · 2015-06-11T01:30:13

The length of the missing side is exactly #2sqrt11#.

Use the Pythagorean theorem #c^2=a^2+b^2#, where #c# is the hypotenuse of a right triangle, and #a# and #b# are sides or legs of the right triangle.

For this question:

#c=4sqrt3#
#a=2#
#b=?#

Solve the Pythagorean theorem for #a#.

#b^2=c^2-a^2#

#b^2=(4sqrt3)^2-2^2# =

#b^2=16(3)-4# =

#b^2=48-4=44#

#b=sqrt44# =

#b=sqrt(4xx11)# =

#b=2sqrt11#