How do you find the missing sides and angles in the right triangle, where a is the side across from angle A, b across from B, and c across from the right angle given a = 28, c = 42?

Question

11699 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-17T22:00:21

See below.

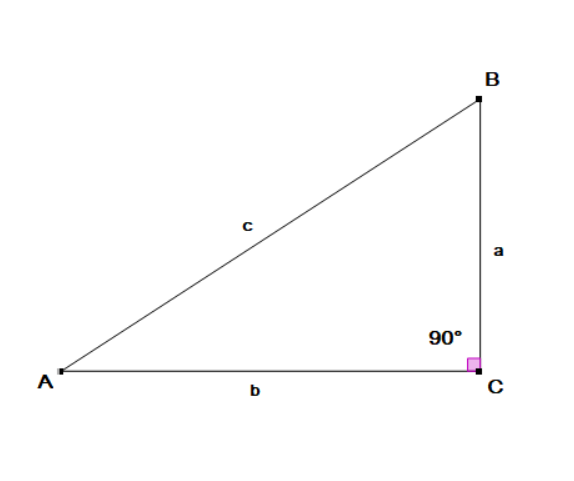
enter image source here

First we need to find side b

Pythagoras Theorem states:

#a^2+b^2=c^2#

So:

#b^2=c^2-a^2#

#:.#

#b^2=(42)^2-(28)^2=1764-784=980=>b=sqrt(980)=14sqrt(5)#

There are a few different ways of finding the remaining angles, this is just one of them.

#tanA=a/b#

#:.#

#tanA=28/(14sqrt(5))=2/sqrt(5)=(2sqrt(5))/5#

#A = tan^-1(tanA)=tan^-1((2sqrt(5))/5)=41.81^o#

Angle B

The sum of the angles in a triangle add up to #180^o#

#:.#

#180^o-(41.81^o + 90^o)=48.19^o#

Full solution:

#A=41.81^o#

#B=48.19^o#

#C=90^o#

#a=28#

#b=14sqrt(5)~~31.3#

#c=42#