Question

How do you find the set of parametric equations for the line in 3D described by the general equations x-y-z=-4 and x+y-5z=-12?

Answer 1

The parametric equations are:

`{ (x=6lamda), (y=4/3+4lamda), (z=8/3+2lamda) :}`

Explanation:

The two equations represent planes `Pi_1`, and `Pi_1`, say, so the line `L` being sought is the line of intersection of those planes (assuming they do actually intersect).

There are a couple of approaches to this question, but this is the my preferred method from 3D vector analysis. It is slightly longer than other approaches but it helps gain a fuller understanding of vector planes, normals and lines:

The normal vector to a plane is given by the coefficients of `x`, `y` and `z`, so:

`Pi_1: \ \ x-y-z=-4 \ \ \ \ => vec(n_1) = ( (1), (-1), (-1) )`
`Pi_2: \ \ x+y-5z=-12 => vec(n_2) = ( (1), (1), (-5) )`

Then the direction of the line, `L` is that of the cross product of the above normal vectors (as it will be perpendicular to both the normal vectors, ie parallel to both planes). So our direction vector is:

`vec(d) = ( (1), (-1), (-1) ) xx ( (1), (1), (-5) )`
`\ \ \ \ = | (hat(i), hat(j), hat(k)), (1,-1,-1), (1,1,-5) |`
`\ \ \ \ = ( (+,{(-1)(-5)-(1)(-1)}), (-,{(1)(-5)-(1)(-1)}), (+,{(1)(1)-(1)(-1)}) )`
`\ \ \ \ = ( (5+1), (-(-5+1)), (1+1) )`
`\ \ \ \ = ( (6), (4), (2) )`

And so as we have the direction vector, we can form the equation of the line:

`L: \ \ vec(r) = vec(a)+ lamda( (6), (4), (2) )`

To find `vec(a)` we need a coordinate on the line. Let us arbitrarily put `x=0` in both plane equations, so;

`Pi_1: \ \ -y-z = -4`
`Pi_2: \ \ y-5z \ \ \ = -12`

If we solve these equations by adding them we get:

`-6z=-16 => z=8/3`

And back substitution gives `y=4/3`, And so `( (0), (4/3), (8/3) )` lies on both planes, Hence the required equation is:

`L: \ \ vec(r) = ( (0), (4/3), (8/3) )+ lamda( (6), (4), (2) )`

To convert this from vector to parametric from we simply expand for a generic point `vec(r) = ((x), (y), (z))` to get:

`((x), (y), (z)) = ( (0), (4/3), (8/3) ) + lamda( (6), (4), (2) ) = ( (6lamda), (4/3+4lamda), (8/3+2lamda) )`

Hence the parametric equations are:

`{ (x=6lamda), (y=4/3+4lamda), (z=8/3+2lamda) :}`

This 3D plot shows the planes, the normals, and the line of intersection:

Answer 2

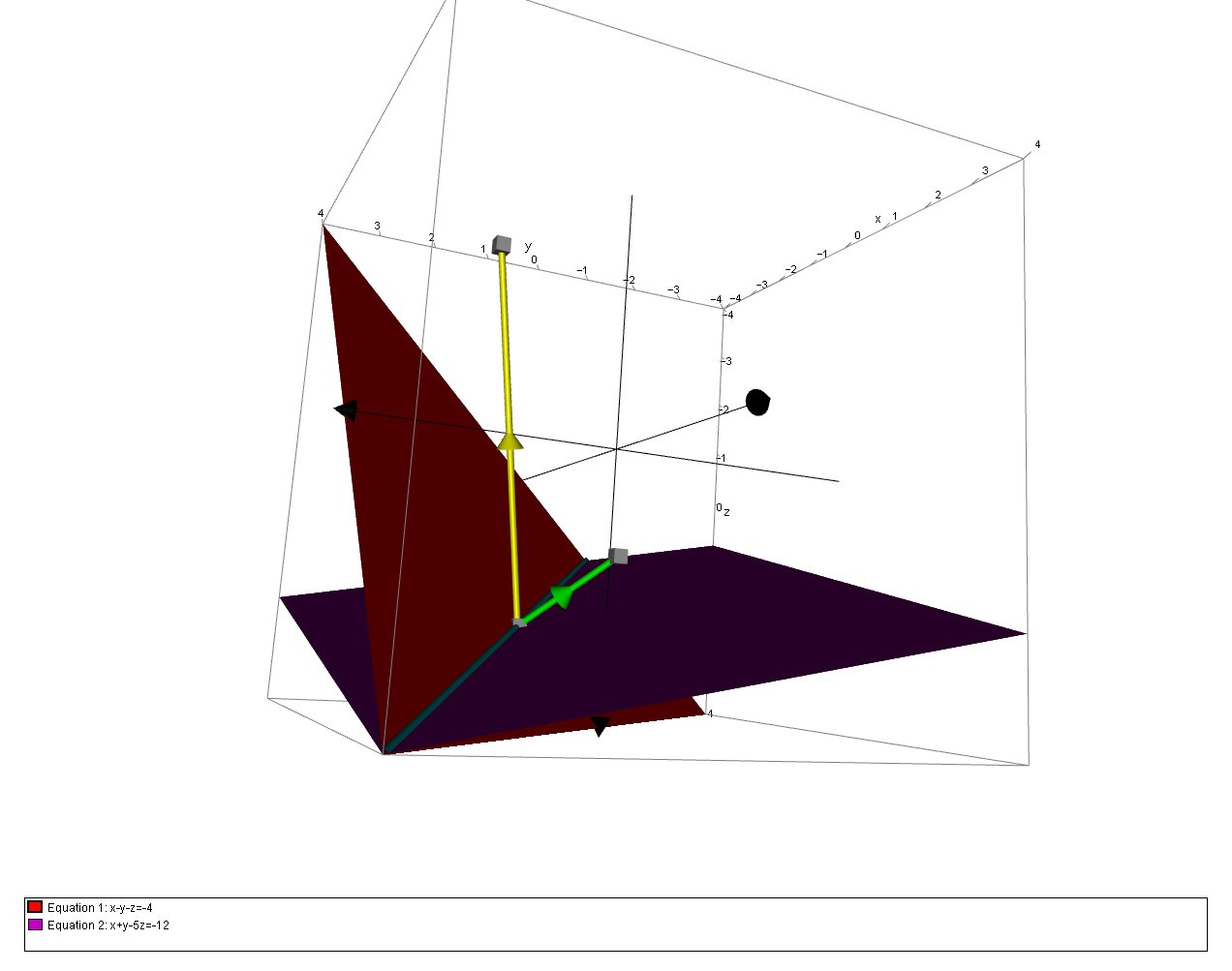
The reqd. Parametric Eqns. of the Line are :

`x=3k-8, y=2k-4, z=k. k in RR.`

Explanation:

Observe that the reqd. Line, say, `L` has been described as the

intersecting Line of two planes

`pi_1 : x-y-z=-4, and, pi_2 : x+y-5z=-12.`

`pi_1+pi_2 rArr 2x-6z=-16, i.e., x-3z=-8.`

`rArr (x+8)/3=z.......................(1)`

`pi_1-pi_2 rArr -2y+4z=8 rArr -y+2z=4.`

`rArr z=(y+4)/2......(2)`

From `(1) and (2), (x+8)/3=(y+4)/2=z, i.e.,`

`(x-(-8))/3=(y-(-4))/2=(z-0)/1.`

Hence, the Parametric Eqns. of `L` are as follows ;

`x=3k-8, y=2k-4, z=k. k in RR.`