How do you find the slope and intercept of #y = -5x + 2#?
2 Answers
Explanation:
This equation is in slope-intercept form:
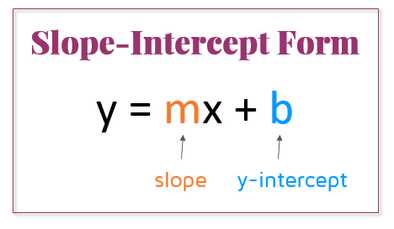
Based on the image, we know that the slope is the value multiplied by
To find the
Subtract
Divide both sides by
The
To find the
The
Hope this helps!
Slope
Explanation:
The good thing is that this equation is in slope-intercept form
What about the
The
Therefore, our slope is
Hope this helps!


