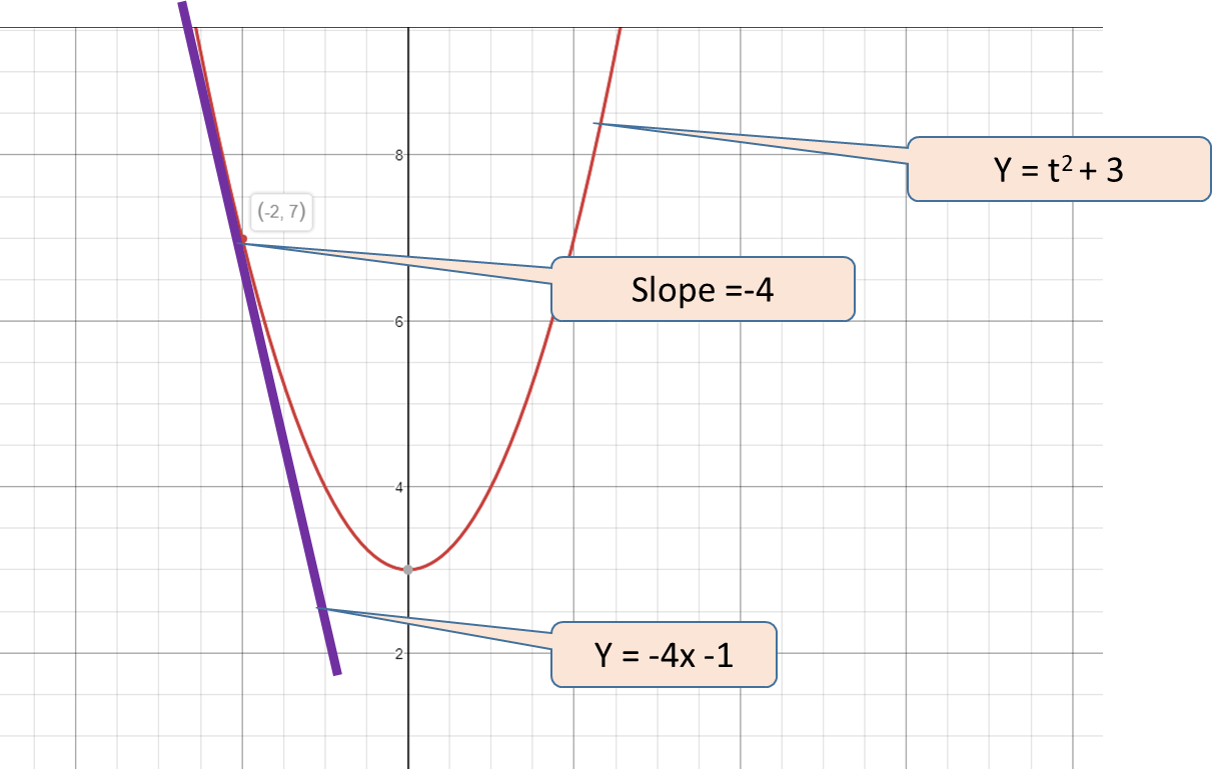
How do you find the slope of the tangent line to the graph of the function #h(t)=t^2+3# at (-2,7)?

Question

46662 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-06-30T05:30:34

The equation of the tangent is -

#y=-4x-1#

Given -

#h(t)=t^2+3#

Let us have it as -

#y=t^2+3#

Its slope at any point is given by its first derivative.

#dy/dx=2t#

Slope of the curve exactly at #x=-2# is-

#dy/dx=2(-2)=-4#

The tangent is passing through the point #(-2,7)#

The slope of the tangent at Point #x=-2# is the same as slope of the curve at that point #(-2,7)#

#m=-4#
#x=-2#
#y=7#
#mx+c=y#
#(-4)(-2)+c=7#
#8+c=7#
#c=7-8=-1#

The equation of the tangent is -

#y=-4x-1#

enter image source here