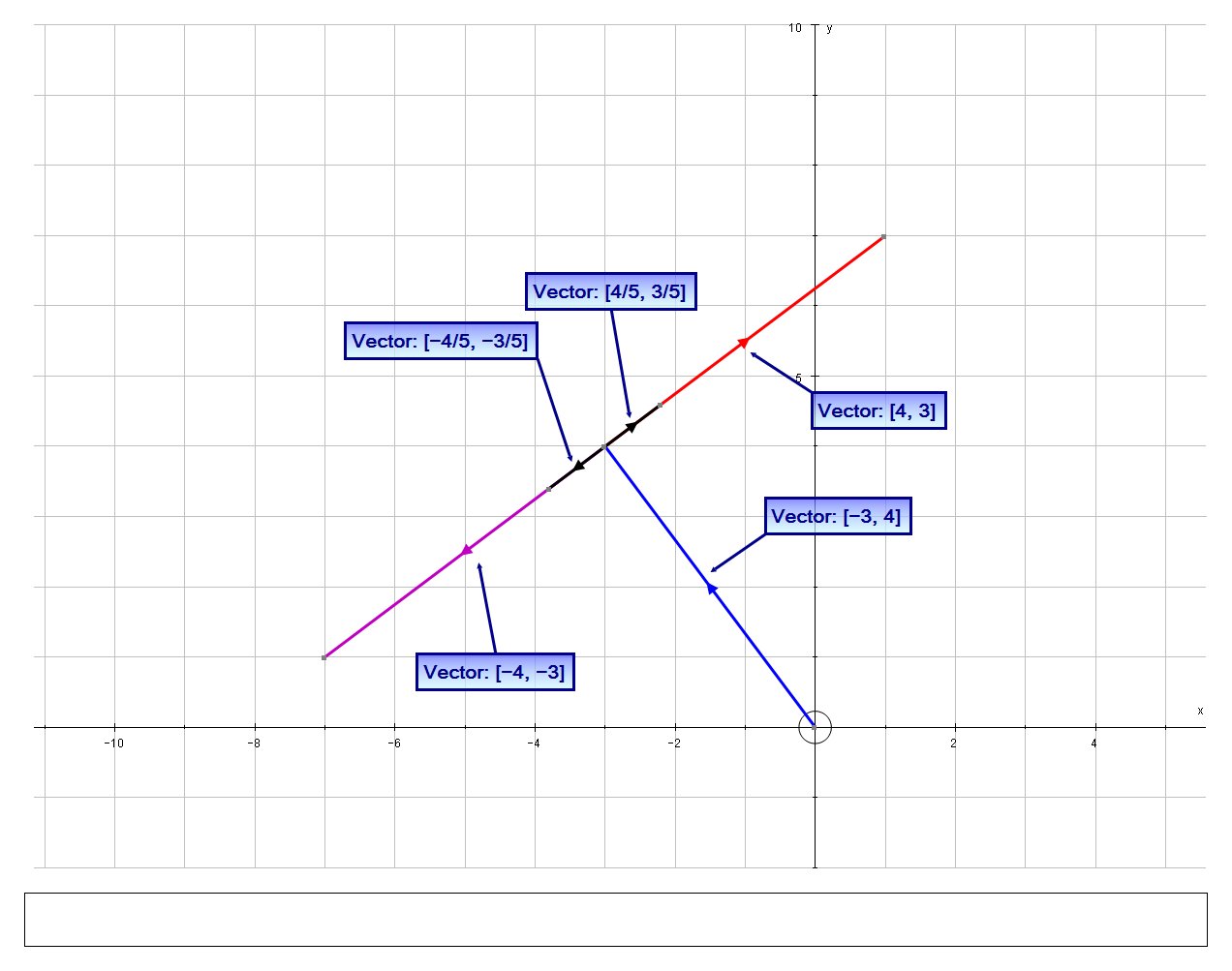
How do you find two unit vectors that are orthogonal to (-3,4)?
2 Answers
I got:
#color(blue)(hatv = << 4/5,3/5,0 >>)#
#color(blue)(hatw = << 0,0,-1 >>)#
assuming that the vectors all have to be orthogonal to each other (so the two vectors we found are orthogonal to each other as well).
Note that we could have also used any of the following pairs:
#color(blue)(hatv = << -4/5,-3/5,0 >>)#
#color(blue)(hatw = << 0,0,-1 >>)#
#color(blue)(hatv = << 4/5,3/5,0 >>)#
#color(blue)(hatw = << 0,0,1 >>)#
#color(blue)(hatv = << -4/5,-3/5,0 >>)#
#color(blue)(hatw = << 0,0,1 >>)#
Try drawing these out and see if you can see where I'm getting this.
Orthogonal means
THE FIRST VECTOR
One way to generate the first vector orthogonal to
For a clockwise rotation of
#hatR = [(costheta,sintheta),(-sintheta,costheta)]#
Plug in
#hatR = [(cos90^@,sin90^@),(-sin90^@,cos90^@)]#
#= [(0,1),(-1,0)]#
So:
#hatR[(3),(4)]#
#= [(0,1),(-1,0)][(-3),(4)]#
#= << 4,3 >>#
And you can see that they are orthogonal by checking the dot product:
#<< -3, 4 >> cdot << 4, 3 >>#
#= -3*4 + 4*3 = -12 + 12 = 0# #color(blue)(sqrt"")#
You can also check by drawing out the actual vector on the xy-plane.
THE SECOND VECTOR
The second vector orthogonal to these can be found from taking the cross product of the two vectors we now have. Try converting the vectors to a sum of unit vectors
#<< -3, 4 >> = -3hati + 4hatj#
#<< 4, 3 >> = 4hati + 3hatj#
Their cross product is then:
#(-3hati + 4hatj)xx(4hati + 3hatj)#
#= -12cancel(hatixxhati)^(0) - 9hatixxhatj + 16hatjxxhati + 12cancel(hatjxxhatj)^(0)#
#= -9hatk - 16hatixxhatj#
#= -9hatk - 16hatk#
#= -25hatk#
#= << 0,0,-25 >># where we use the identities
#hatixxhatj = hatk# and#hatixxhatj = -hatjxxhati# .
Then, the two vectors we evaluated before must be projected onto three dimensions. Let us set them on the
#<< -3,4,0 >>#
#color(green)(<< 4,3,0 >>)#
#color(green)(<< 0,0,-25 >>)#
TURNING THE VECTORS INTO "UNIT VECTORS"
The two vectors we found were not unit vectors though, and are just vectors. So, we just have to normalize them now:
#hatv = (<< 4,3,0 >>)/(|| << 4,3,0 >> ||)#
#= (<< 4,3,0 >>)/(sqrt(4^2 + 3^2 + 0^2))#
#= (<< 4,3,0 >>)/5#
#= << 4/5,3/5,0 >>#
Similarly, for the other one:
#hatw = (<< 0,0,-25 >>)/(||<< 0,0,-25 >>||)#
#= (<< 0,0,-25 >>)/25#
#= << 0,0,-1 >>#
So, the two unit vectors orthogonal to
#color(blue)(hatv = << 4/5,3/5,0 >>)#
#color(blue)(hatw = << 0,0,-1 >>)#
NOTE: If you continue to normalize the original provided vector to get
The unit vectors are:
# << 4/5, 3/5>> # and# << -4/5, -3/5>> #
Explanation:
Suppose a suitable orthogonal vector in
# << a, b>>#
If this vector is orthogonal to
# << a, b>> * << -3,4 >> = 0 #
# :. -3a+4b = 0 #
We now need to find suitable values of
Arbitrarily choose
# :. -12+4b = 0 =>. b=3 #
Arbitrarily choose
# :. 12+4b = 0 =>. b=-3 #
Hence two orthogonal vectors are:
# << 4, 3>> # and# << -4, -3>> #
We now need to normalise the vectors (as the question asked for unit vectors):
In both cases:
# |<< 4, 3>>| = |<< -4, -3>>| = sqrt(16+9) = 5 #
We can normalise the vectors by multiplying by
Hence, the unit vectors are:
# << 4/5, 3/5>> # and# << -4/5, -3/5>> #