Question

How do you graph `f(x)= abs(x-6)`?

Answer 1

I like graphing using piece-wise functions.

Let's write two piecewise functions, one for the area of the function where `y` is decreasing, another for the part where `y` is increasing.

The function will change from a decrease to an increase at the vertex. When given an absolute value function of the form `y = a|x - p| + q`, the vertex is at `(p, q)`.

Since `p = 6` and `q= 0`, `f(x) = |x - 6|` has its vertex at `(6, 0)`.

The next step is to determine the range. This will be determined by two elements:

a) The y-coordinate of the vertex
b) The direction of opening

In the function `y = |x - 6|`, the vertex has a y-coordinate of `0` and the function opens upward (since parameter `a` is positive).

Hence, the range of this function is `y ≥ 0`.

Now that we know the vertex, we can find another point on the graph and then find the equation of both piece-wise functions. I think it may be simplest to find the y-intercept of the function.

`y = |x - 6|`

`y = |0 - 6|`

`y = |-6|`

`y = 6`

Hence, the y-intercept is at `(0, 6)`. Start by finding the slope between the two points we found.

`m = (y_2 - y_1)/(x_2 - x_1)`

`m = (6 - 0)/(0 - 6)`

`m = 6/(-6)`

`m = -1`

We need to find the equation using point slope form now.

`y - y_1 = m(x - x_1)`

`y - 6 = -1(x - 0)`

`y - 6 = -x`

`y = -x + 6`

This is the left-hand side equation, since `y` is decreasing due to the negative slope. You will graph this line paying attention to the range, `y ≥ 0` (you must stop the line once you hit the line y = 0#).

As for the right-hand side piecewise equation, this can be obtained by multiplying the `mx +b` side of the left-hand piece-wise function by `-1`.

`y = -(-x + 6)`

`y = x - 6`

In summary, our piecewise equations to graph are `y = x - 6, x ≥ 6` and `y = -x + 6, x < 6`.

You should have gotten a graph similar to the following.

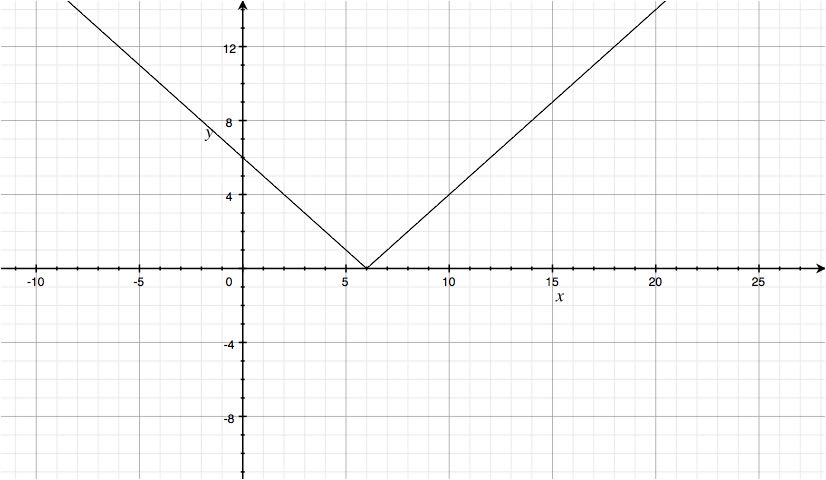
Hopefully this helps!