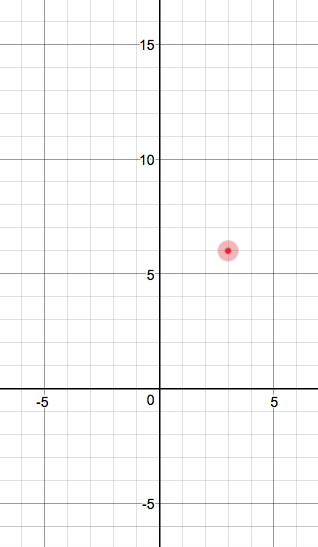
Since this is in vertex form, #a(x - h)^2 + k#, we could first plot the vertex. The coordinates of the vertex are #(h, k)#, and, comparing our function #g(x) = (x - 3)^2 + 6# to the general vertex form, we get that our vertex is at #(3, 6)#:
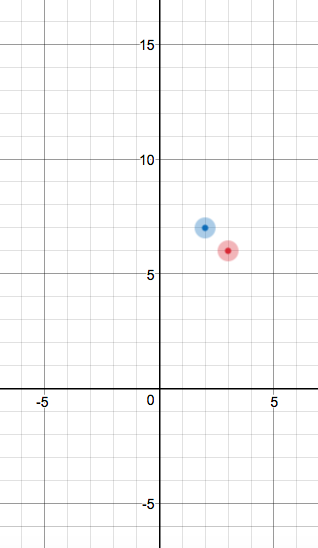
Now, we could simply try some other values of #x# and see where they would end up in the plane. A definition of the vertex, however, is the point on the axis of symmetry, meaning that what is on the left side mirrors on to the right side of the vertex.
Let's try #x = 2#:
#g(2) = (2 - 3)^2 + 6#
#= (-1)^2 + 6#
#= 1 + 6#
#= 7#
So we have point #(2, 7)#:
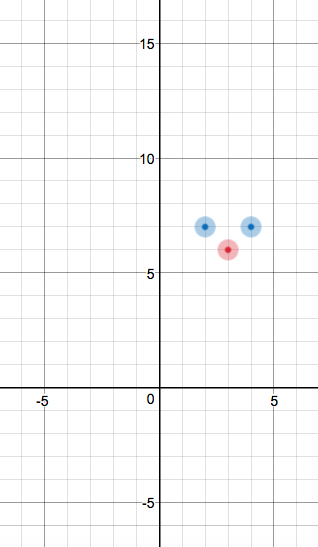
How about #x = 4#?
#g(4) = (4 - 3)^2 + 6#
#= (1)^2 + 6#
#= 1 + 6#
#= 7#
We get #(4, 7)#:
As you can see, there is symmetry! #x = 2# is simply #1# unit to the left from the vertex, and #x = 4# is #1# unit to the right from the vertex. We could use this property to our advantage so that we don't have to calculate twice.
Now we can try #x = 1#:
#g(1) = (1 - 3)^2 + 6#
#= (-2)^2 + 6#
#= 4 + 6#
#= 10#
Plotting #(1, 10)#:
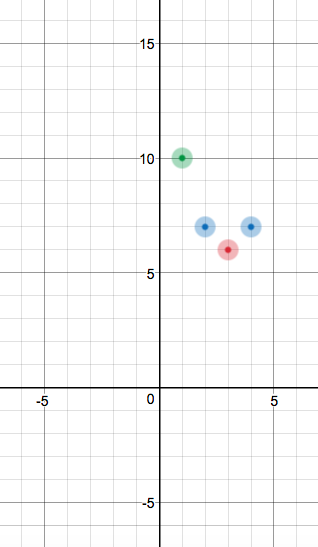
Since #1# is #2# units away from #3#, the #y#-value for #x = 5# should also be #10#, because #5# is also #2# units away from #3#.
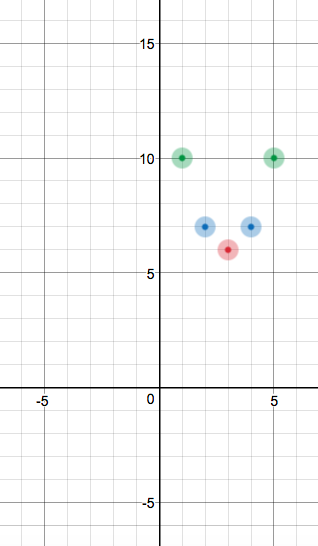
Let's do our last two points: #x = 0# and #x = 6#. We're getting to the #y#-intercept here!
#g(0) = (0 - 3)^2 + 6#
#= (-3)^2 + 6#
#= 9 + 6#
#= 15#
So the #y#-intercept is at #(0, 15)#:
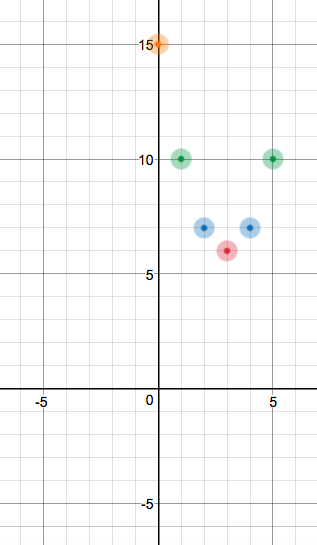
And then there should also be #(6, 15)# due to symmetry:

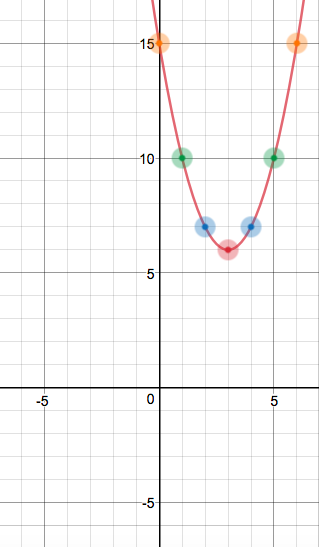
Now, we could be plotting more and more points; in fact, that's what a graph is: a visual representation between variables, and a function is graphed by plotting all possible points! However, at this point, we should be able to estimate the parabola: