How do you graph #r = 2#?
1 Answer
Dec 13, 2015
You can change it to rectangular coordinates or consider that is the graph produced by a point at distance
Explanation:
Consider the following diagram:
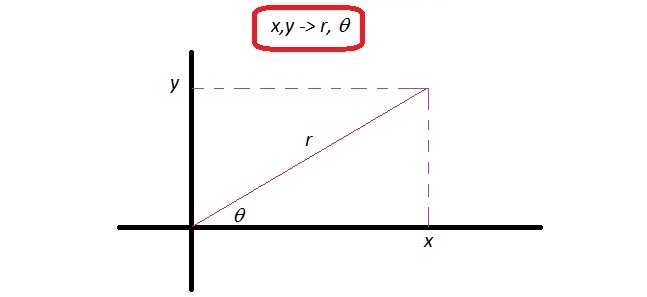
We can see that the relationships between rectangular and polar coordinates are:
and:
In your case you have:
Change it into rectangular to get:
Square both sides:
Which is the equation of a circle of radius

