Graphing Basic Polar Equations
Key Questions
-
Limacons are polar functions of the type:
#r=a+-bcos(theta)#
#r=a+-bsin(theta)#
With#|a/b|<1# or#1<|a/b|<2# or#|a/b|>=2# Consider, for example:
#r=2+3cos(theta)#
Graphically:
Cardioids are polar functions of the type:
#r=a+-bcos(theta)#
#r=a+-bsin(theta)#
But with#|a/b|=1# Consider, for example:
#r=2+2cos(theta)#
Graphically:
in both cases:
#0<=theta<=2pi# .....................................................................................................................
I used Excel to plot the graphs and in both cases to obtain the values in the#x# and#y# columns you must remember the relationship between polar (first two columns) and rectangular (second two columns) coordinates: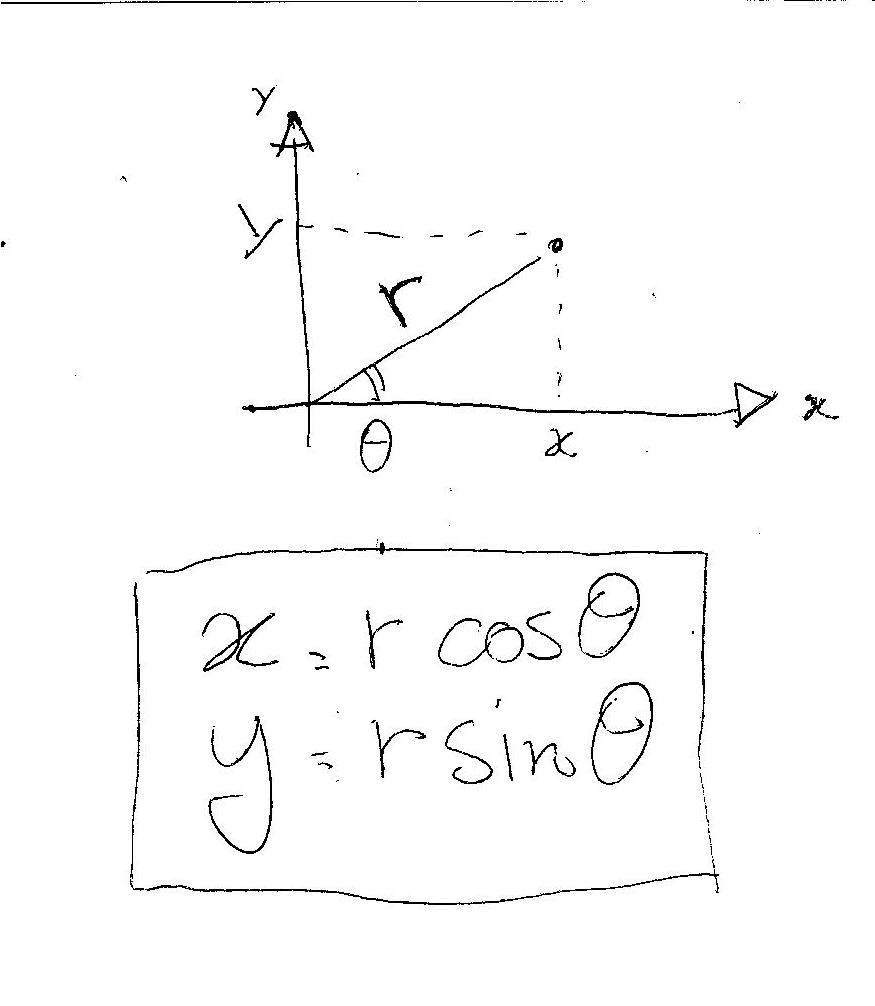
-
You can find a lot of information and easy explained stuff in "K. A. Stroud - Engineering Mathematics. MacMillan, p. 539, 1970", such as:
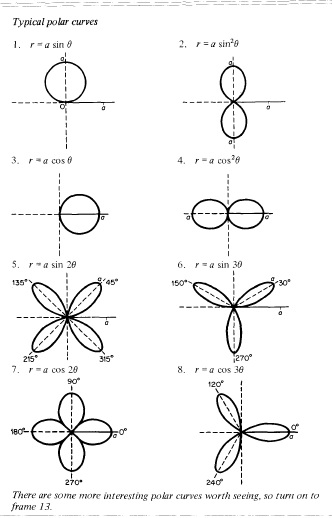
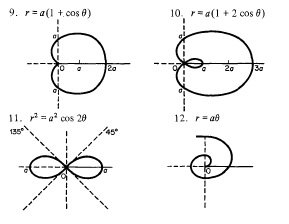
If you want to plot them in Cartesian coordinates remember the transformation:
#x=rcos(theta)#
#y=rsin(theta)# For example:
in the first one:#r=asin(theta)# choose various values of the angle#theta# evaluate the corresponding#r# and plug them into the transformation equations for#x and y# . Try it with a program such as Excel... it is fun!!! -
You consider a function of the type:
#r=f(theta)# So you give values of the angle
#theta# and the function gives you values of#r# .To graph polar functions you have to find points that lie at a distance
#r# from the origin and form (the segment#r# ) an angle#theta# with the#x# axis.
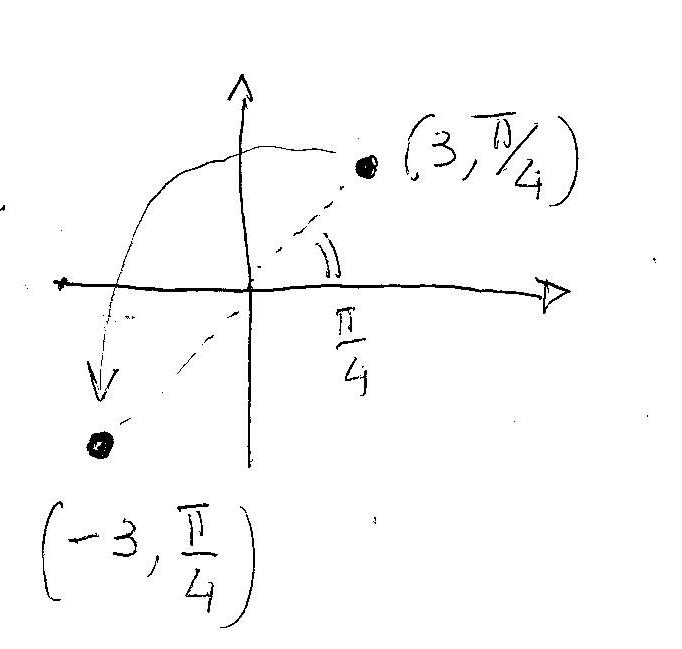
Take for example the polar function:
#r=3# This function describes points that for every angle
#theta# lie at a distance of 3 from the origin!!!Graphically:
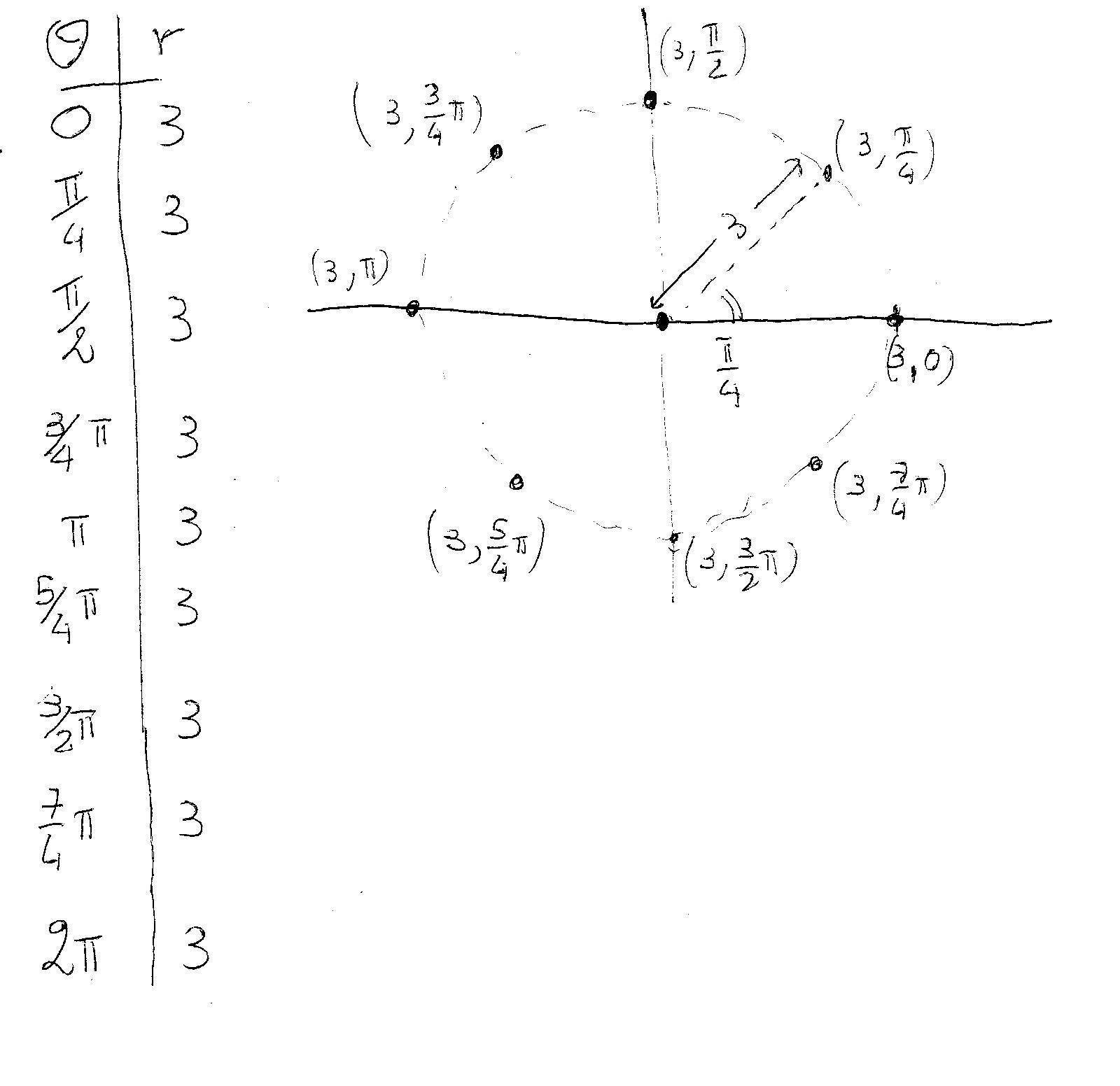
The result is a circle of radius#r=3# .Now, the only complication is when
#r# becomes NEGATIVE ...how do I plot this?
We use a trick....we take the positive and flip it about the origin!!!!!!
Take for example the polar function:
#r=-3# This function describes points that for every angle
#theta# lie at a distance of...-3 from the origin????
We use our trick!Graphically:
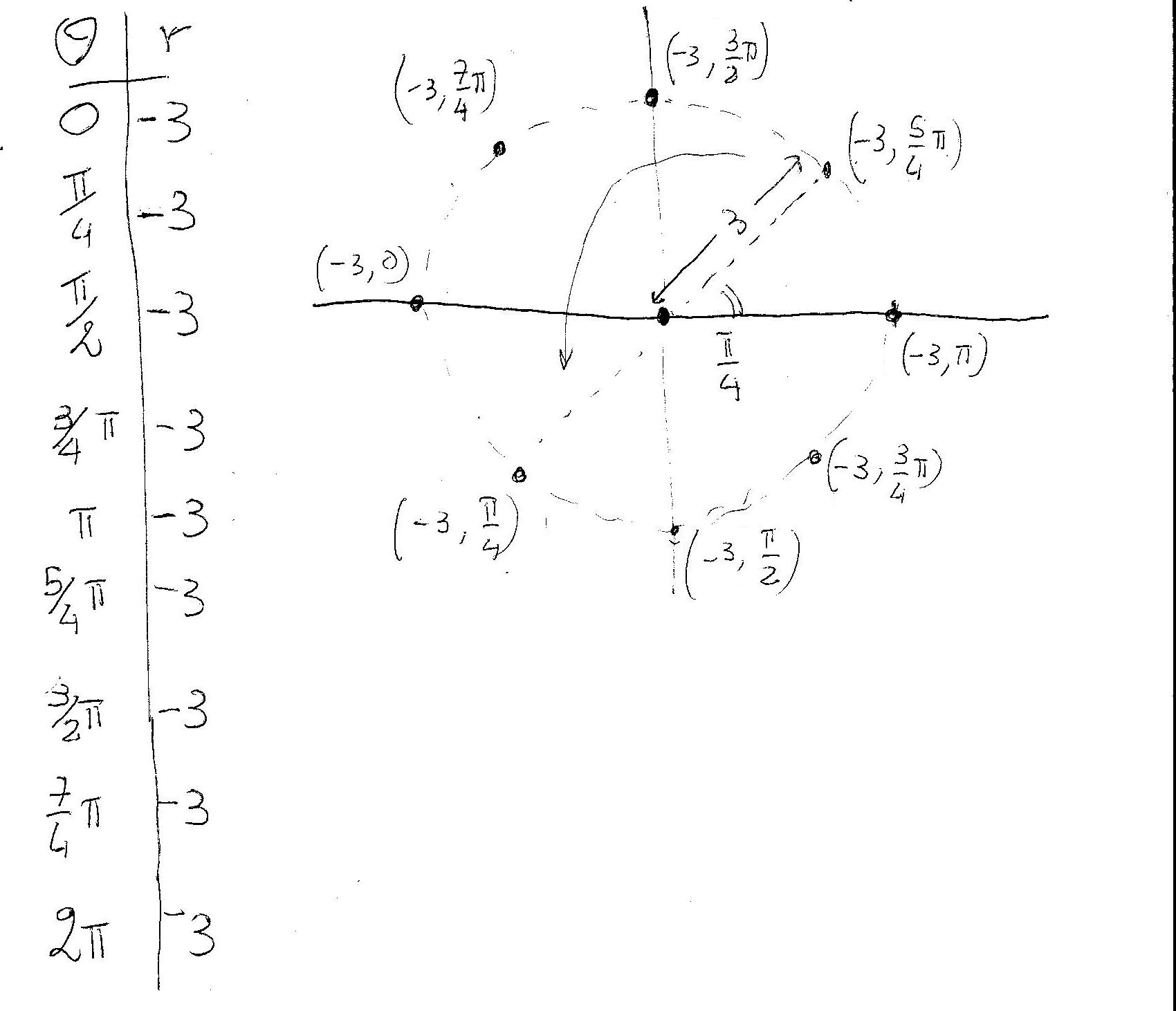
Every point of the old graph flipped about the origin!!!!
It is a circle...again!!!!Now try by yourself with:
#r=2cos(theta)#
Build a table of#theta# and#r# and plot it...you should get another circle but with its center....on the#x# axis (in#(1,0)# ) and radius =1.There are more complicated (and graphically beautiful) polar functions such as limacons, cardioids, roses, lemniscates, etc…try them!!!