How do you graph #r^2=2sin(3θ)#?
1 Answer
Thanks to Sam's updating, it is a 3-petal curve, without using non-negative r, For the three loops, choose the ranges
Explanation:
Upon insertion of the graph by Sam, I have duly revised my answer,
to make the answer almost perfect..
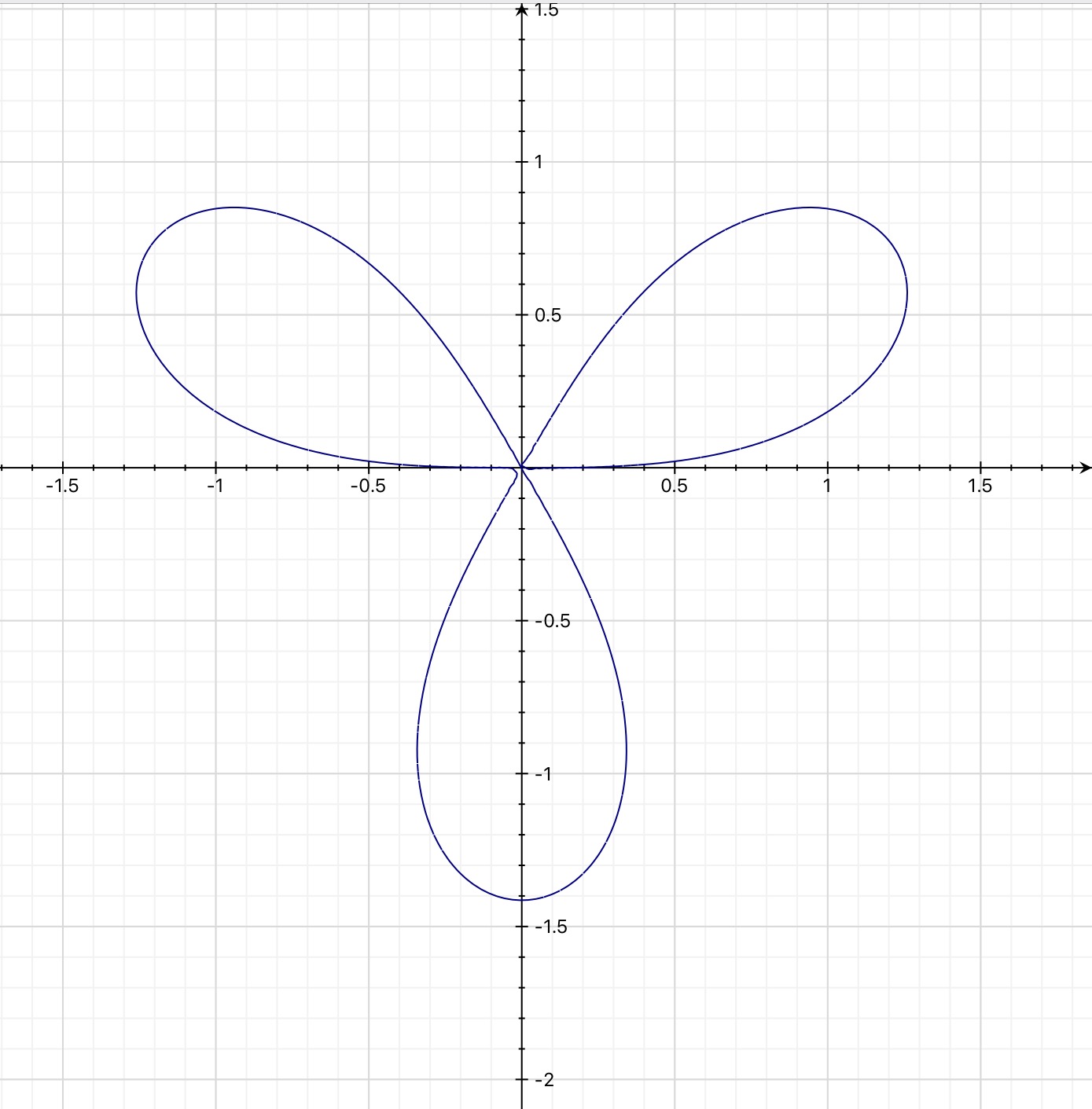
Choose the range
so that
positive. It is similar, for the the other two petals, in the respective
ranges for
For every
(If negative r is allowed, there would be six loops altogether, keeping
As the period of
when the ends of the intervals for
multiple
