How do you graph #r^2 theta=1#?
1 Answer
May 14, 2016
Choosing
the graph is a spiral through
Explanation:
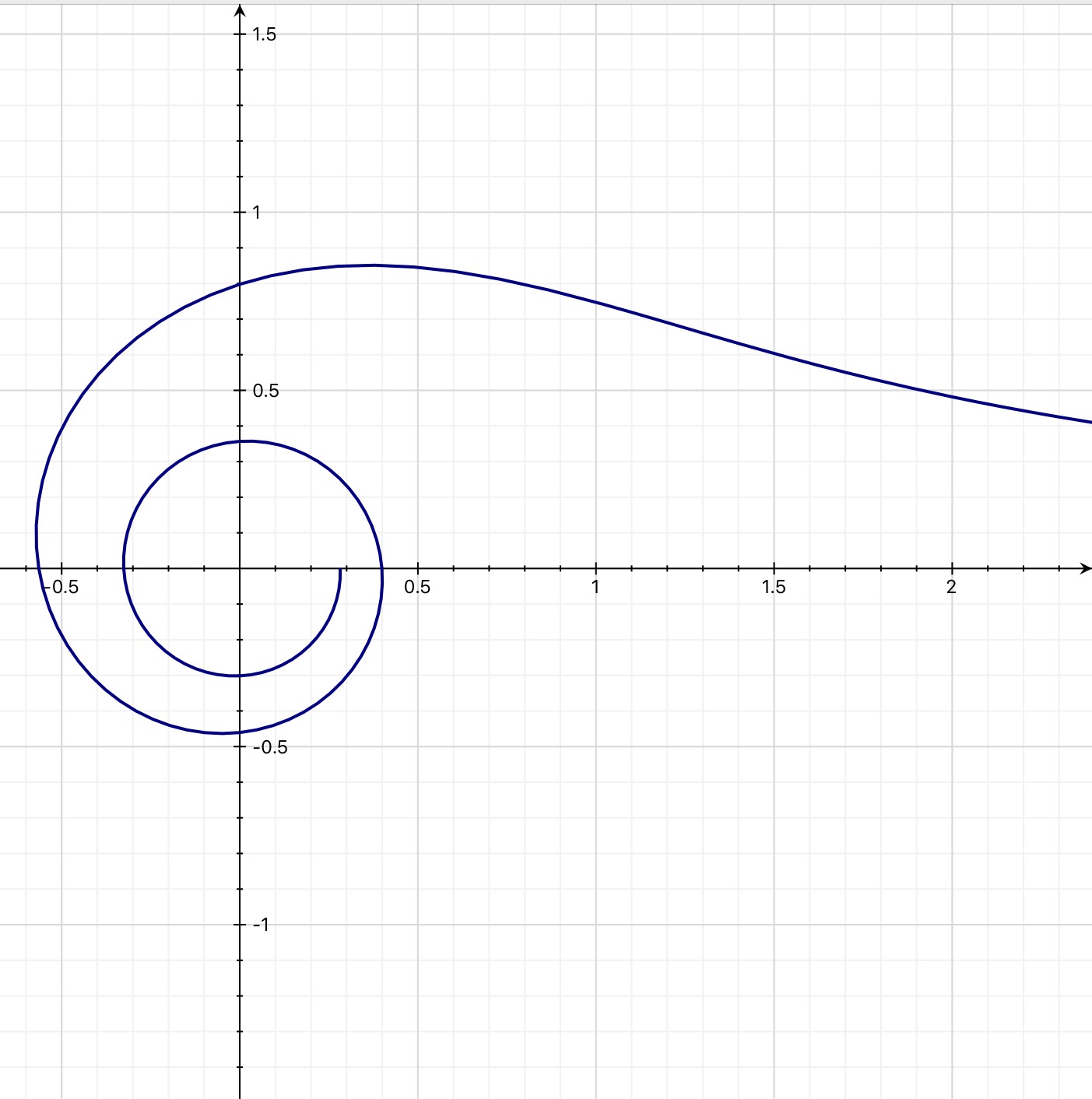
If negative r is allowed,
The each graph is the mirror image of the other with respect to the pole r = 0.
Choosing
the graph is a spiral through
