Question

How do you graph the polar equation `r=1.5theta`?

Answer 1

Polar equations vary `r` as `theta` cycles counterclockwise through from `0` to `2pi`, `2pi - 4pi`, etc.

`r = 1.5theta`

This equation has `r` increase by `1.5` for every `1` radian that we pass through (`(180/pi)^@`). If `r = theta`, we would have gotten a spiral.

Here, with `r = 1.5theta` in `[0,8pi]`, we just have a bigger spiral:

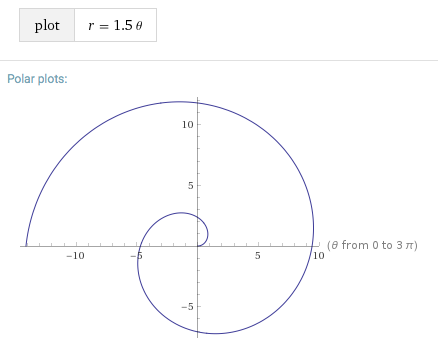
For example, if you look at `theta = pi/2`, you should see

`r = 1.5 xx pi/2 ~~ ul2.35` on the vertical axis.

If we pass through `pi/2` radians, we move to

`r = 1.5 xx (pi/2 + pi/2) => ul(-4.71)` on the horizontal axis

If we pass through `(3pi)/2` radians, we move to

`r = 1.5 xx (pi/2 + pi) => ul(-7.07)` on the vertical axis.

If we pass through `2pi` radians, we move up to

`r = 1.5 xx (pi/2 + (3pi)/2) ~~ ul9.42` on the horizontal axis.

Then, if we pass through `(5pi)/2` radians, we move up to

`r = 1.5 xx (pi/2 + 2pi) ~~ ul11.78` on the vertical axis.

Once you have those major points, connect them in a spiral.