How do you graph using slope and intercept of #2x+y=8#?
1 Answer
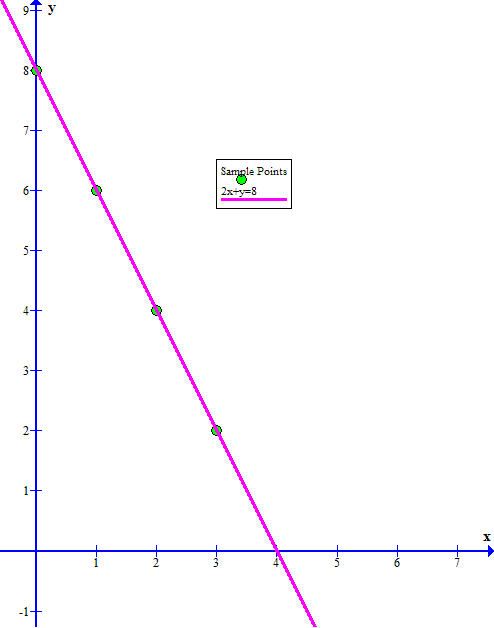
(see below for method used in generating this graph)
Explanation:
The slope of a line in the form
The y-intercept is the value of
In this case
and
Based on the
The slope of
So we can build a table of a few Sample points:
Plotting these coordinates on the Cartesian plane and drawing a straight line through them should give a graph that looks like the Answer above.
