How do you graph using slope and intercept of #3x-y=2#?
1 Answer
Please read the explanation.
Explanation:
We are given the liner equation:
The standard form of a linear equation in the slope-intercept form is:
We rewrite the linear equation
Subtract
Multiply both sides of the equation by
We now have our linear equation in the slope-intercept form:
Slope
Slope can also be defined as (Change in y)/(change in x)
On a graph, plot the point on the y-axis, at the point
From this point
Join these two points to get the required graph:
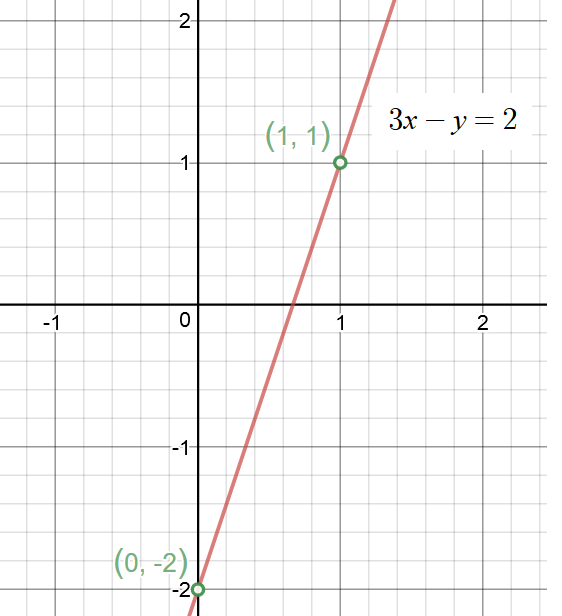
Hope it helps.

