Question

How do you make the graph for `y=ln(1+x/(ln(1-x)))`?

Answer 1

It looks to me like Socratic graphing cannot plot it for some reason.
This is the graph:

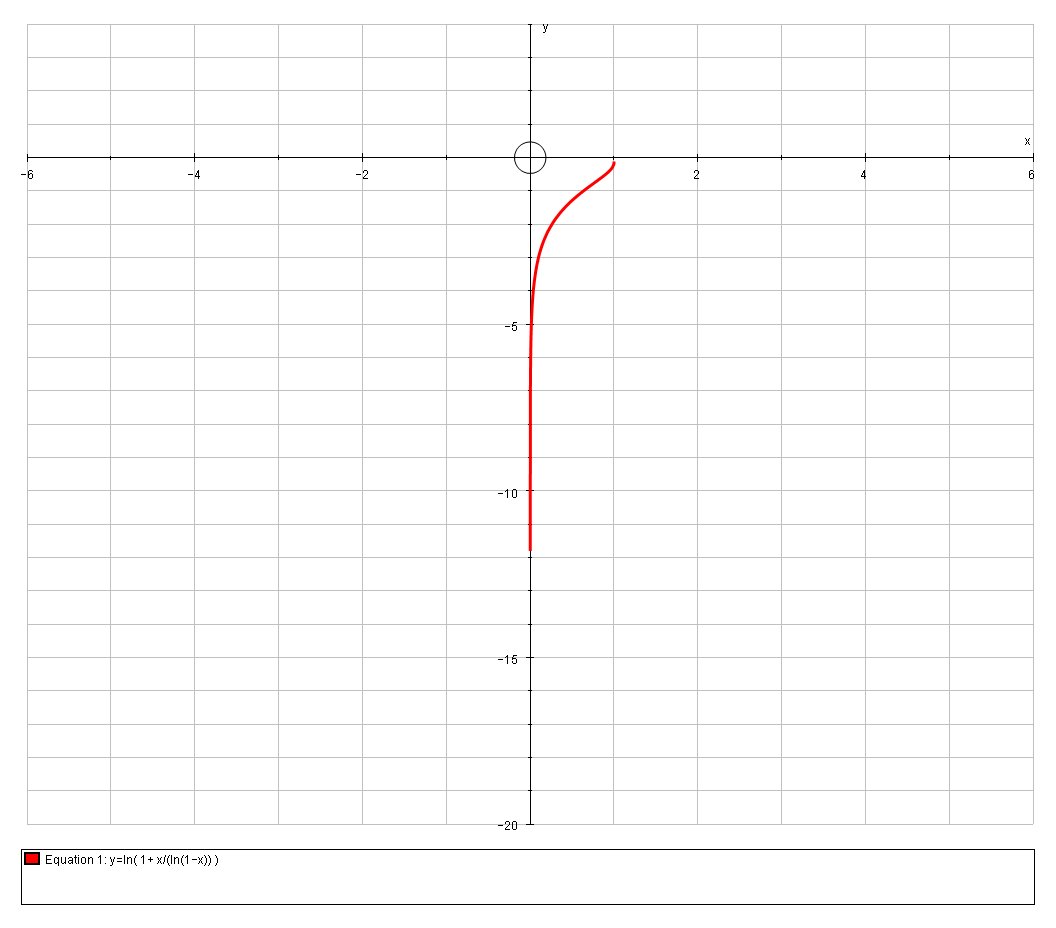
And my calculator can plot it also:

Answer 2

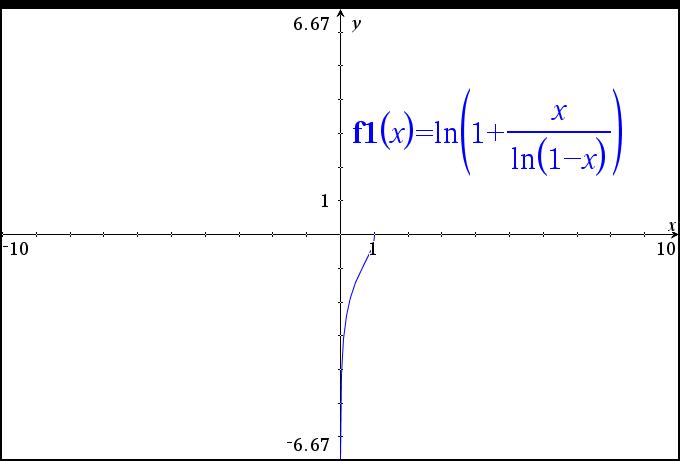
See Socratic graph and explanation.

Explanation:

To make y real, `1-x > 0`, giving `x < 1` and

`1+x/ln(1-x)>0`, giving

`x/ln(1-x) > -1`, with `x < 1`.

So, if `x in (0, 1), ln(1-x)<0`, and so,

`x<-ln(1-x)<=1`. This gives

`x>=1-e^(-1)=0.63212`, nearly.

Also, the upper terminal of the graph is `(1_1, 0_-)` and the lower

end is `(1-1/e, -1)`.

Now, `x in [1-1/e, 1)`, the the graph is illustrative of this aspect of the

function. I realize that the lower end is lower than `(1-1/e, -1)`.

I hope that , with the interest already shown, Steve could study my

answer and give his comments.

graph{x-(e^y-1)ln(1-x)=0 [-2.5, 2.5, -1.25, 1.25]}

@a-s-adikesavan

I've embedded my comments in the answer rather than as a comment due to all the maths:

For the domain of the function:

Condition 1

`1-x>0` so that `ln(1-x) in RR => color(red)(x<1)`
This is consistent with your answer

Condition 2
I get a different result for the 2nd condition; as follows'

`1+x/ln(1-x) > 0` so that `ln(1+x/ln(1-x)) in RR`

As we are solving an inequality we need to be careful with the sign of the denominator `ln(1-x)` and change the inequality direction as appropriate.

Using the fact that for any `A in RR`:

`ln A \ \ \ { (>0), (=0), (<0) :} \ \ iff {: (A>1), (A=1), (A<1) :}`

Lets examine the three cases:

Case 1: `\ \ color(blue)(ln(1-x)>0)`

`ln(1-x)>0 =>1-x>1=>x<0`
With this requirement, we have:
`1+x/ln(1-x) > 0`
`:. ln(1-x)+x>0` (as `ln(1-x)>0`)
And this has no real solutions:

Case 2: `\ \ color(blue)(ln(1-x)=0)`

`ln(1-x)=0 =>1-x=1=>x=0`
This case would lead to `x/ln(1-x)` being of an indeterminate form `0/0`, so lets use L'Hôpital's rule to find the limit:
`lim_(x rarr 0)(1+x/ln(1-x)) = 1+lim_(x rarr 0)(x/ln(1-x))`
`" "= 1+lim_(x rarr 0)(1/(1/(1-x)(-1)))`
`" "= 1-1`
`" "= 0`
and as we require `1+x/ln(1-x)>0` we can eliminate this.

Case 3: `\ \ color(blue)(ln(1-x)<0)`

`ln(1-x)<0 =>1-x<1=>x>0`
With this requirement, we have:
`1+x/ln(1-x) > 0`
`:. ln(1-x)+x<0` (as `ln(1-x)<0`)
Using WFA and graphs this has the solution `color(red)(x>0)`

Combining all the results gives the domain of `y` as `x in (0,1)`, which is inconsistent with your analysis.

Thanks to some help from @jimh we have

`lim_(x rarr 0)ln(1+x/ln(1-x)) rarr -oo`

But it does so extremely slowly due to the effect of the `log` function, and so the range is `y in (-oo,0)`

Due to the fact that very rapidly we can be dealing with very small numbers with many decimal places, the computer accuracy is a issue when displaying the graph of the function.

Eg `A~~1xx10^-10 => ln(A) ~~ -23` so the graph appear to "tail off" in the region `-25 lt y lt -15` but this is an illusion and for a sufficiently small `x`then `y` decreases without bound.

Other than looking at derivatives I'm not sure there is much more to add