Question

How do you show that the curve x=cos t , y= sin t cos t has two tangents at (0,0) and find their equations?

Answer 1

The equations are the two tangents are:

`y = +- x`

Explanation:

We have parametric equations:

`x = cost`
`y = sintcost \ \ \` where `t in [0,2pi]`

Firstly, as most modern calculators have (and examinations allow) graphing capabilities, let us look at the graph of the curve.

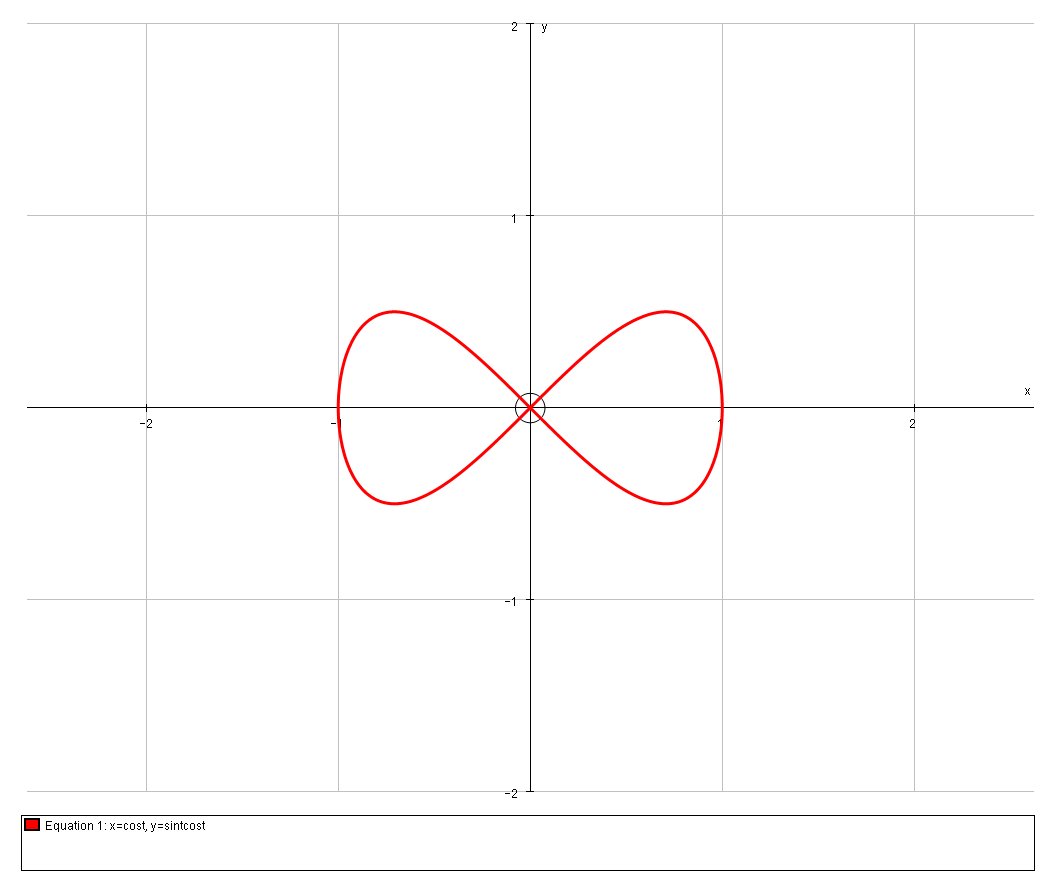
So certainly it appears that at the origin there would be two tangents, so now let us prove this:

The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. (If needed, then the normal is perpendicular to the tangent so the product of their gradients is `−1`).

Differentiating the equations wrt `t` we get:

`dx/dt = -sint`
`dy/dt = sint(-sint)+(cost)(cost) = cos^2t-sin^2t`

And so the curves derivative is given by:

`dy/dx = (dy/dt)/(dx/dt) = -(cos^2t-sin^2t)/sint`

At the origin we clearly have simultaneously:

`x = y = 0`

`:. cost = 0 => t = pi/2, (3pi)/2`

And with these values of `t`, the corresponding values of the derivative are:

`[ dy/dx ]_(t=pi/2) = (0-1)/1 = 1`

`[ dy/dx ]_(t=(3pi)/2) = (0-(-1))/(-1) = -1`

And there are no other values of `t` in the range `[0,2pi]`, showing there are two values of `dy/dx` at the origin, from which we conclude there are two tangents at the origin.

So the tangents pass through `(0,0)` and has gradient `m_(T1)=1`, and `m_(T2)=1` and using the point/slope form `y-y_1=m(x-x_1)` the tangent equations we seek are;

When `t=pi/2`:

`y - 0 = (1)(x-0 )`
`y=x`

When `t=(3pi)/2`:

`y - 0 = (-1)(x-0 )`
`y=-x`

Answer 2

I like Steve's solution better than mine. But, for what it's worth, here's my solution.

Explanation:

`x = cost` and `y = sintcost`

With `x = cost`, there are two possibilities for `sint`,

`sint = +-sqrt(1-x^2)`

So `y = +-xsqrt(1-x^2)`

And `dy/dx = +-(sqrt(1-x^2)-x^2/sqrt(1-x^2))`

At `x = 0`, we get two values for `dy/dx`, namely `+-1`.

The equation s of the lines are `y = +-x`

Although not needed, here are the graphs of the two branches.

`y = xsqrt(1-x^2)` is shown below

graph{xsqrt(1-x^2) [-3.08, 3.08, -1.538, 1.54]}

`y = -xsqrt(1-x^2)` is shown below

graph{-xsqrt(1-x^2) [-3.08, 3.08, -1.538, 1.54]}