Question

How do you sketch the graph by determining all relative max and min, inflection points, finding intervals of increasing, decreasing and any asymptotes given `f(x)=x^4-4x^3`?

Answer 1

See below.

Explanation:

`f(x) = x^4-4x^3` `" "` Domain `(-oo,oo)`

Asymptotes: None. Polynomials don't have (linear) asymptotes.

Intercepts
`x`-intercepts are at solutions to `f(x) = 0`, so the `x` intercepts are `0` and `4`.
`y`-intercepts are at `f(0)` so the `y`-intercept is `0`.

Analysis of `f'(x)`

`f'(x) = 4x^3-12x^2` is never undefined and is `0` at `x=0` and at `x=3`. Investigating the sign of `f'(x)` we find

on `(-oo,0)`, `f'(x)` is negative, so `f` is decreasing,
on `(0,3)`, `f'(x)` is negative, so `f` is decreasing,
on `(3,oo)`, `f'(x)` is positive, so `f` is increasing.

There is a relative minimum at `x=3`. The minimum is `f(3) = 3(3)^3-4(3)^3 = -27`

There are no relative maxima.

Before we look at concavity, here is the straight line sketch:

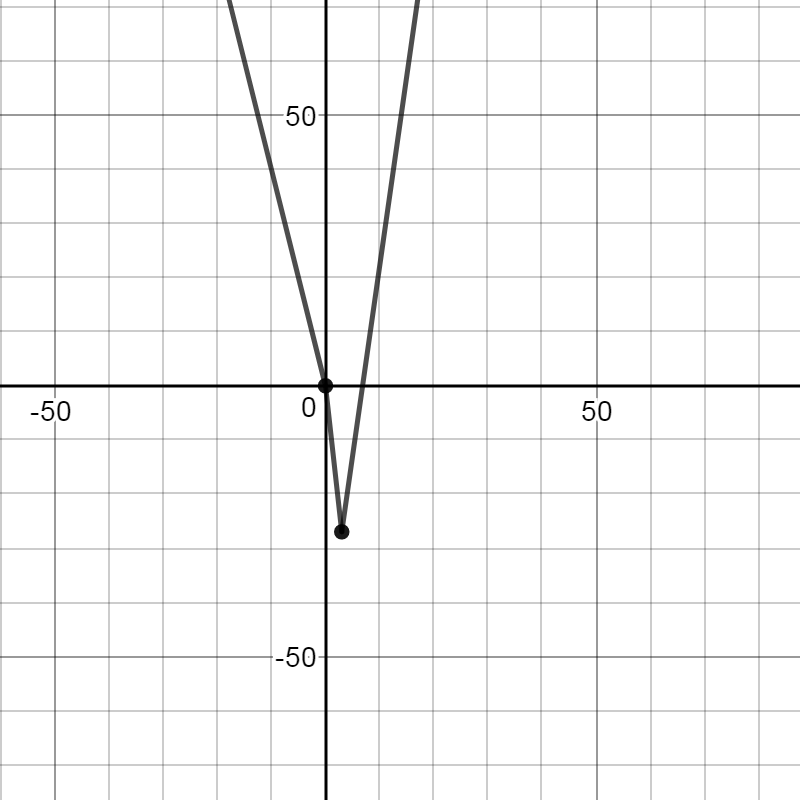
Analysis of `f''(x)`

`f''(x) = 12x^2-24x = 12x(x-2)` is never undefined and is `0` at `x=0` and at `x=2`. Investigating the sign of `f''` we have

on `(-oo,0)`, `f''(x)` is positive, so `f` is concave up (convex),
on `(0,3)`, `f''(x)` is negative, so `f` is concave down (concave),
on `(3,oo)`, `f''(x)` is positive, so `f` is concave up (convex).

Inflection points are points on the graph at which the concavity changed. Therefore, there are inflection points at `x=0` and `x=2`.

The inflection points are: `(0,0)` and `(2,-16)`.

(`f(2) = 2(8)-4(8) = -16)`.

Now that we have concavity, we can improve our sketch:

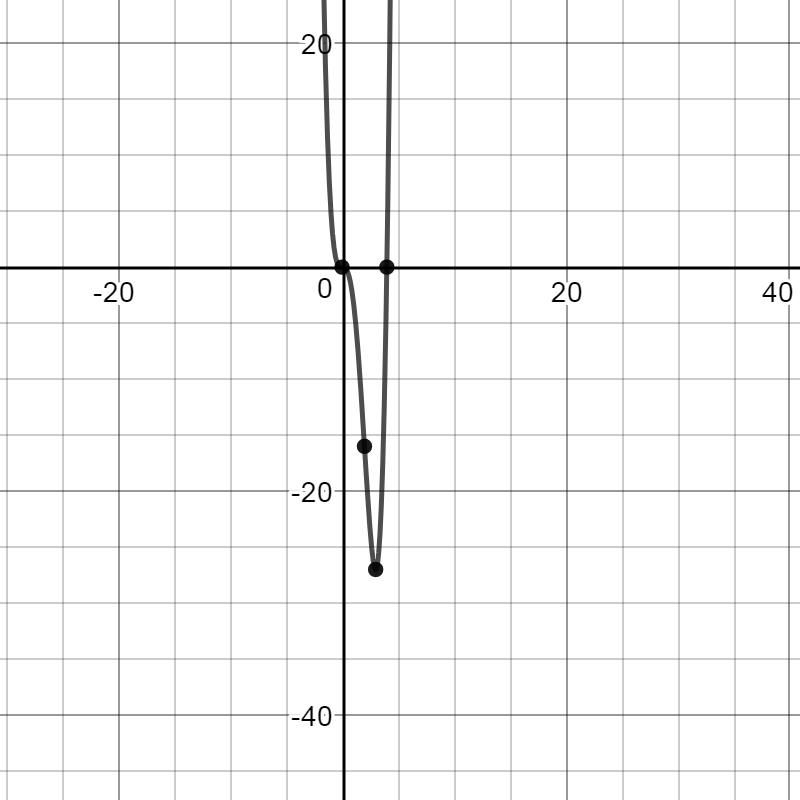
Here is Socratic's graph. (You can move it and zoom in/out. If you leave this answer and come back, the graph will reset to the original view.)
graph{x^4-4x^3 [-37.2, 35.86, -29.07, 7.48]}