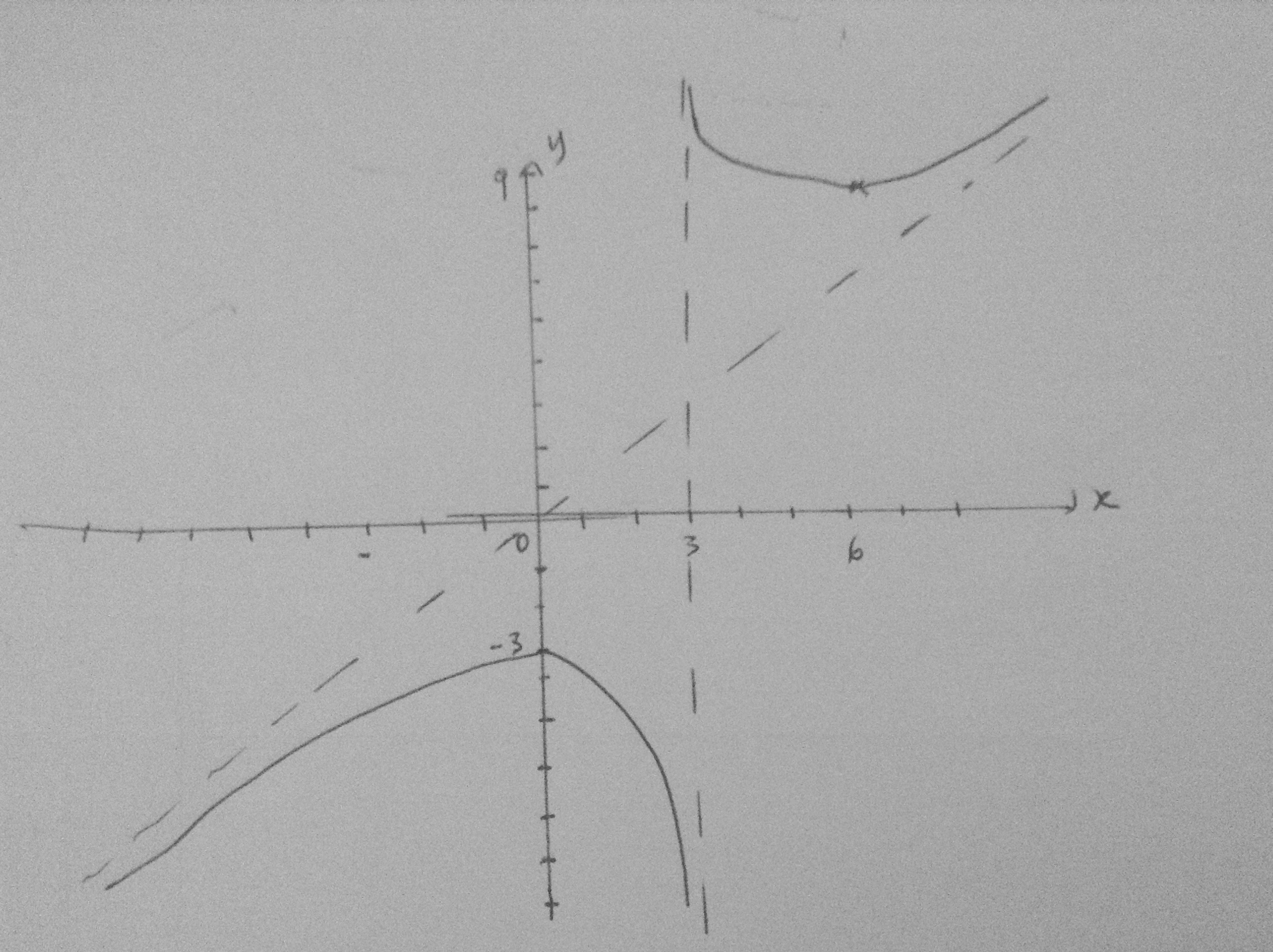#f(x) = (x^2 - 3x + 9)/(x - 3) = (x^2 - 3x)/(x - 3) + 9/(x - 3)#
#= (x(x - 3))/(x - 3) + 9/(x - 3) = x + 9/(x - 3)#
So you actually wanna sketch #f(x) = x + 9/(x - 3)#
Domain:
The domain of this function is all Real x except 3
because #9/(x - 3) # would become unreal!
This brings us to Asymptotes:
They're two Asymptotes:
No 1: #y = x# because as #x -> oo # # f(x) -> x#
No 2: #x= 3# is a vertical asymptote because as #f(x) -> oo # # f(x)-> 3#
Next, turning points:
To find turning points (maxima and minima),
We let# y = f(x) => y = x + 9/(x - 3)#
We make #x# the subject of the equation,
#=> yx - 3y = x^2 - 3x + 9#
#=> x^2 -(3 + y)x + 9+ 3y = 0#
Since all the values of #x# are real, #b^2 - 4ac >= 0#
#=> (3 + y)^2 - 4(9 + 3y) >= 0#
#=> y^2 - 6y - 27 >=0 => (y - 9)(y + 3)>= 0#
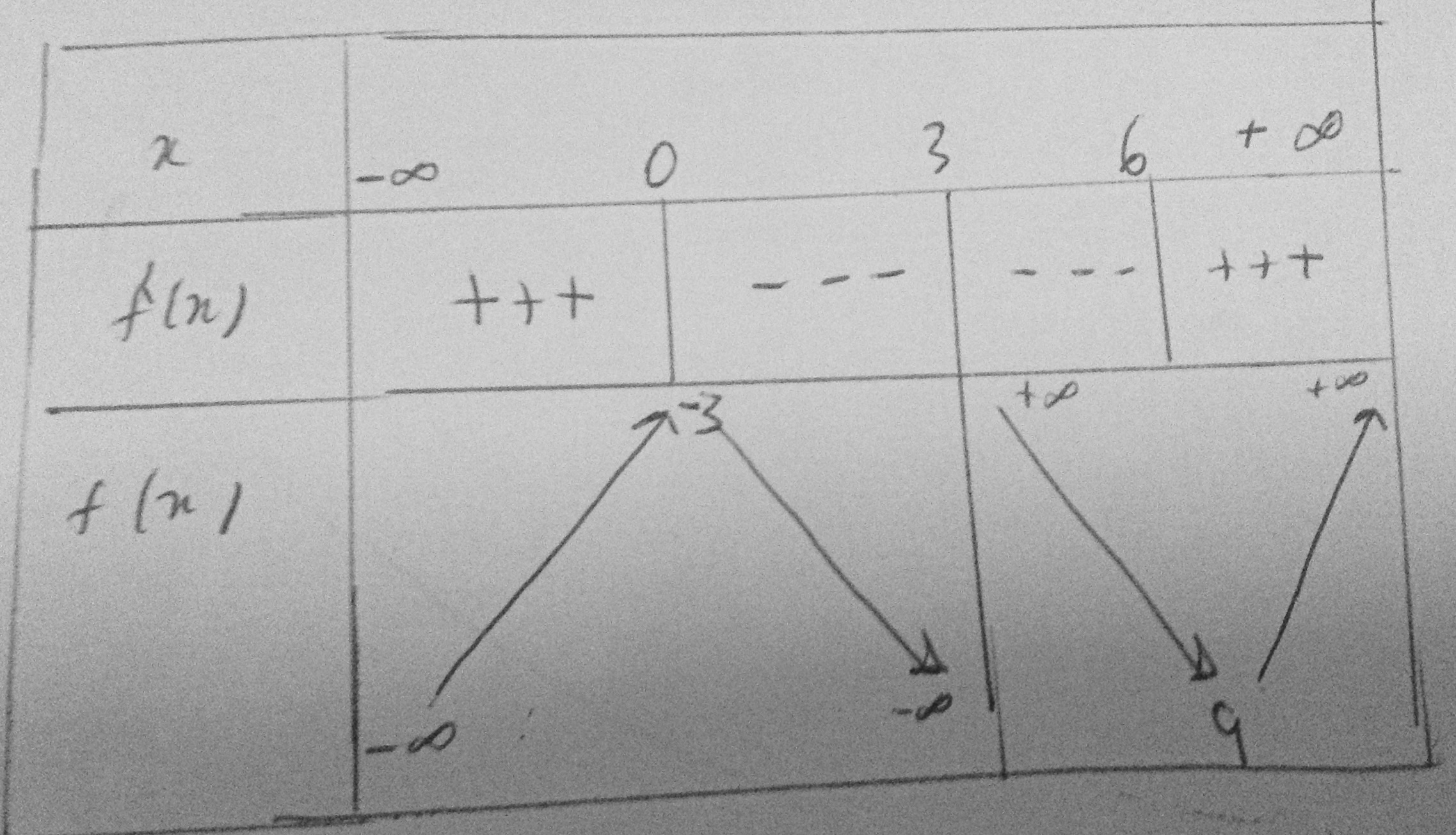
Hence, #y<=-3 uu y >= 9#
Putting the values of #y# in #f(x)# to get #x#
we have the points #(0, -3)# maximum and #(6, 9)# as minimum
To find the intercepts :
#y#- intercept is when #x = 0# we have #(0, -3)#
#x#- intercept is when #y = 0# but #y# cannot be #0#(see the range above)
Table of variation:
So now we're all set to sketch that graph;
Here's what i got: