How do you solve #13x^2-5x<=0#?

Question

1742 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-12T15:47:45

Solve as a regular quadratic and then select test points.

#13x^2 - 5x = 0#

#x(13x - 5) = 0#

#x = 0 and 5/13#

#color(blue)("Test point 1"-> "-1")#

#13(-1)^2 - 5(-1) ≤^? 0#

#18≤^O/ 0#

This inequality is obviously not true, so let's go on to test point #2#.

#color(red)("Test point 2" -> "1/4"#

#13(1/4)^2 - 5(1/4) <=^? 0#

#-0.4375 <= 0#

Hence, the interval that is the solution to this inequality #0<= x <= 5/13#.

On a number line, the solution would be the turquoise rectangle.

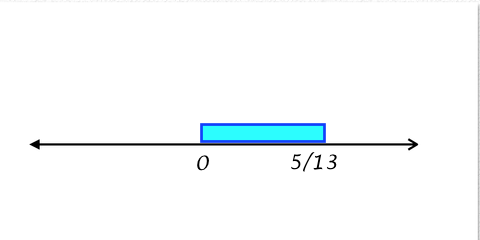
enter image source here

Hopefully this helps!