How do you solve #(3x-1)/x<=-1# using a sign chart?
1 Answer
Sep 12, 2016
Explanation:
The first thing you have to do is to rewrite the disequation in a form like:
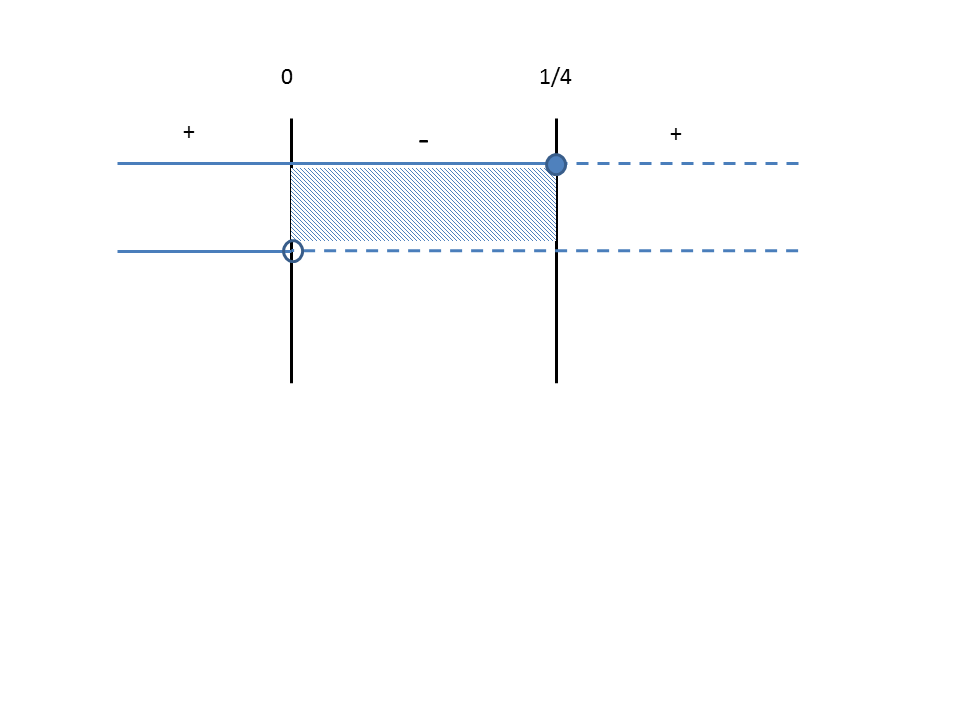
Now you could find the values of
Now you can draw the sign chart: where the single disequation are satisfied use a continuos line, else a discontinuos line. Where both the lines will be continuos or discontinuos the sign is
The sign of disequation is