How do you solve #6/x+2>=0# using a sign chart?
1 Answer
Nov 9, 2016
Explanation:
First solve the inequality as if it were an equality:
Set the numerator equal to zero to find where the function intersects the x axis and changes signs, and set the denominator equal to zero to find where the function has an asymptote and (possibly) changes signs.
Numerator:
Denominator:
Now put the values on a number line and test values around them, and check if they are positive or negative.
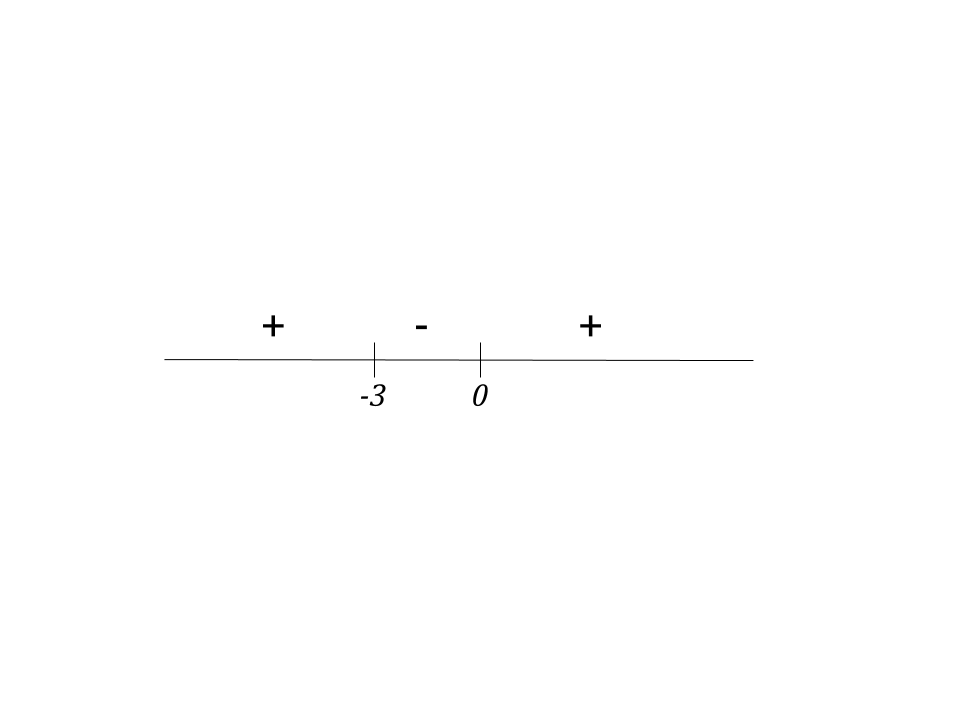
The question asks where is the function greater than or equal to 0, so, the answer is:

